Content (algebra)
In algebra, the content of a polynomial with integer coefficients is the greatest common factor of its coefficients. Thus, e.g., the content of 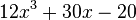 equals 2, since this is the greatest common factor of 12, 30, and -20. The definition may be extended to polynomials with coefficients in any fixed unique factorization domain.
equals 2, since this is the greatest common factor of 12, 30, and -20. The definition may be extended to polynomials with coefficients in any fixed unique factorization domain.
A polynomial is primitive if it has content unity.
Gauss's lemma for polynomials states that the product of primitive polynomials (with coefficients in the same unique factorization domain) also is primitive. Equivalently, it may be expressed as stating that for the content of the product of two polynomials is the product of their contents.
See also
References
- B. Hartley; T.O. Hawkes (1970). Rings, modules and linear algebra. Chapman and Hall. ISBN 0-412-09810-5.
- Page 181 of Lang, Serge (1993), Algebra (Third ed.), Reading, Mass.: Addison-Wesley Pub. Co., ISBN 978-0-201-55540-0, Zbl 0848.13001
- David Sharpe (1987). Rings and factorization. Cambridge University Press. pp. 68–69. ISBN 0-521-33718-6.