Constructible topology
In commutative algebra, the constructible topology on the spectrum  of a commutative ring
of a commutative ring  is a topology where each closed set is the image of
is a topology where each closed set is the image of 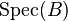 in
in  for some algebra B over A. An important feature of this construction is that the map
for some algebra B over A. An important feature of this construction is that the map 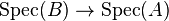 is a closed map with respect to the constructible topology.
is a closed map with respect to the constructible topology.
With respect to this topology,  is a compact,[1] Hausdorff, and totally disconnected topological space. In general the constructible topology is a finer topology than the Zariski topology, but the two topologies will coincide if and only if
is a compact,[1] Hausdorff, and totally disconnected topological space. In general the constructible topology is a finer topology than the Zariski topology, but the two topologies will coincide if and only if 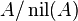 is a von Neumann regular ring, where
is a von Neumann regular ring, where 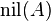 is the nilradical of A.
is the nilradical of A.
See also
References
- ↑ Some authors prefer the term quasicompact here.
- Atiyah, Michael Francis; Macdonald, I.G. (1969), Introduction to Commutative Algebra, Westview Press, p. 87, ISBN 978-0-201-40751-8
- Knight, J. T. (1971), Commutative Algebra, Cambridge University Press, pp. 121–123, ISBN 0-521-08193-9