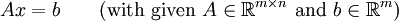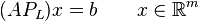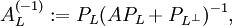Constrained generalized inverse
In linear algebra, a constrained generalized inverse is obtained by solving a system of linear equations with an additional constraint that the solution is in a given subspace. One also says that the problem is described by a system of constrained linear equations.
In many practical problems, the solution  of a linear system of equations
of a linear system of equations
is acceptable only when it is in a certain linear subspace  of
of  .
.
In the following, the orthogonal projection on  will be denoted by
will be denoted by 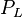 .
Constrained system of linear equations
.
Constrained system of linear equations
has a solution if and only if the unconstrained system of equations
is solvable. If the subspace  is a proper subspace of
is a proper subspace of 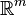 , then the matrix of the unconstrained problem
, then the matrix of the unconstrained problem 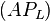 may be singular even if the system matrix
may be singular even if the system matrix  of the constrained problem is invertible (in that case,
of the constrained problem is invertible (in that case, 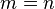 ). This means that one needs to use a generalized inverse for the solution of the constrained problem. So, a generalized inverse of
). This means that one needs to use a generalized inverse for the solution of the constrained problem. So, a generalized inverse of 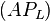 is also called a
is also called a  -constrained pseudoinverse of
-constrained pseudoinverse of  .
.
An example of a pseudoinverse that can be used for the solution of a constrained problem is the Bott-Duffin inverse of  constrained to
constrained to  , which is defined by the equation
, which is defined by the equation
if the inverse on the right-hand-side exists.