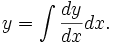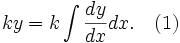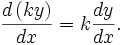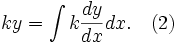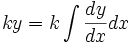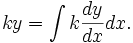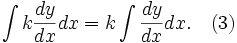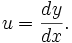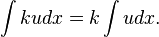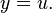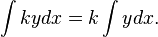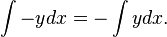Constant factor rule in integration

The constant factor rule in integration is a dual of the constant factor rule in differentiation, and is a consequence of the linearity of integration. It states that a constant factor within an integrand can be separated from the integrand and instead multiplied by the integral. For example, where k is a constant:

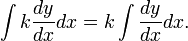
$\int k \frac{dy}{dx} dx = k \int \frac{dy}{dx} dx. \quad$

Proof

Start by noticing that, from the definition of integration as the inverse process of differentiation:

y = \int \frac{dy}{dx} dx.

Now multiply both sides by a constant k. Since k is a constant it is not dependent on x:

ky = k \int \frac{dy}{dx} dx. \quad \mbox{(1)}

Take the constant factor rule in differentiation:

\frac{d\left(ky\right)}{dx} = k \frac{dy}{dx}.

Integrate with respect to x:

ky = \int k \frac{dy}{dx} dx. \quad \mbox{(2)}

Now from (1) and (2) we have:

ky = k \int \frac{dy}{dx} dx

ky = \int k \frac{dy}{dx} dx.

Therefore:

\int k \frac{dy}{dx} dx = k \int \frac{dy}{dx} dx. \quad \mbox{(3)}

Now make a new differentiable function:

u = \frac{dy}{dx}.

Substitute in (3):

\int ku dx = k \int u dx.

Now we can re-substitute y for something different from what it was originally:

y = u. \,

So:

\int ky dx = k \int y dx.

This is the constant factor rule in integration.

A special case of this, with k=-1, yields:

\int -y dx = -\int y dx.