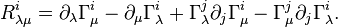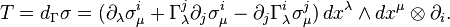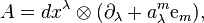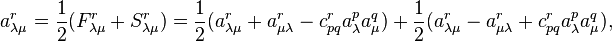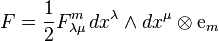Connection (fibred manifold)
In differential geometry, a fibered manifold is surjective submersion of smooth manifolds 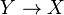 . Locally trivial fibered manifolds are fiber bundles. Therefore, a notion of connection on fibered manifolds provides a general framework of a connection on fiber bundles.
. Locally trivial fibered manifolds are fiber bundles. Therefore, a notion of connection on fibered manifolds provides a general framework of a connection on fiber bundles.
Formal definition
Let 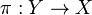 be a fibered manifold. A (generalized) connection on
be a fibered manifold. A (generalized) connection on  is a section
is a section 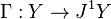 , where
, where 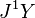 is the jet manifold of
is the jet manifold of  .[1]
.[1]
Connection as a horizontal splitting
Let 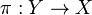 be a fibered manifold. There is the following canonical short exact sequence of vector bundles over
be a fibered manifold. There is the following canonical short exact sequence of vector bundles over  :
:
where 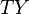 and
and 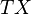 are the tangent bundles of
are the tangent bundles of  , respectively,
, respectively, 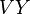 is the vertical tangent bundle of
is the vertical tangent bundle of  , and
, and 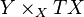 is the pullback bundle of
is the pullback bundle of 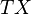 onto
onto  .
.
A connection on a fibered manifold 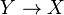 is defined as a linear bundle morphism
is defined as a linear bundle morphism
over  which splits the exact sequence (1). A connection always exists.
which splits the exact sequence (1). A connection always exists.
Sometimes, this connection 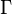 is called the Ehresmann connection because it yields the horizontal distribution
is called the Ehresmann connection because it yields the horizontal distribution
of 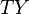 and its horizontal decomposition
and its horizontal decomposition 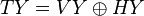 .
.
At the same time, by an Ehresmann connection also is meant the following construction. Any connection 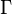 on a fibered manifold
on a fibered manifold 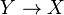 yields a horizontal lift
yields a horizontal lift 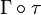 of a vector field
of a vector field 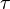 on
on  onto
onto  , but need not defines the similar lift of a path in
, but need not defines the similar lift of a path in  into
into  . Let
. Let ![\mathbb R\supset[,]\ni t\to x(t)\in X](../I/m/c6658c71e39d5c99e630f2899d560407.png) and
and 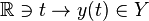 be smooth paths in
be smooth paths in  and
and  , respectively. Then
, respectively. Then 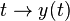 is
called the horizontal lift of
is
called the horizontal lift of 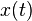 if
if 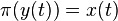 ,
, 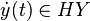 ,
, 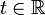 . A connection
. A connection 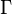 is said to be the Ehresmann connection if, for each path
is said to be the Ehresmann connection if, for each path ![x([0,1])](../I/m/3719838ed629111466697af8e85844ce.png) in
in  , there exists its horizontal lift trough any point
, there exists its horizontal lift trough any point ![y\in\pi^{-1}(x([0,1]))](../I/m/ea1b5a767ad488e0a74252244caa6cb7.png) . A fibered manifold is a fiber bundle if and only if it admits such an Ehresmann connection.
. A fibered manifold is a fiber bundle if and only if it admits such an Ehresmann connection.
Connection as a tangent-valued form
Given a fibered manifold 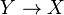 , let it be endowed with an atlas of fibered coordinates
, let it be endowed with an atlas of fibered coordinates 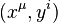 , and let
, and let 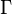 be a connection on
be a connection on 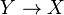 . It yields uniquely the horizontal tangent-valued one-form
. It yields uniquely the horizontal tangent-valued one-form
on  which projects onto the canonical tangent-valued form (tautological one-form)
which projects onto the canonical tangent-valued form (tautological one-form) 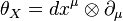 on
on  , and vice versa. With this form, the horizontal splitting (2) reads
, and vice versa. With this form, the horizontal splitting (2) reads
In particular, the connection 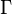 (3) yields the horizontal lift of any vector field
(3) yields the horizontal lift of any vector field 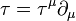 on
on  to a projectable vector field
to a projectable vector field
on  .
.
Connection as a vertical-valued form
The horizontal splitting (2) of the exact sequence (1) defines the corresponding splitting of the dual exact sequence
where 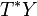 and
and 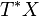 are the cotangent bundles of
are the cotangent bundles of  , respectively, and
, respectively, and 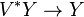 is the dual bundle to
is the dual bundle to 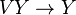 , called the vertical cotangent bundle. This splitting is given by the vertical-valued form
, called the vertical cotangent bundle. This splitting is given by the vertical-valued form
which also represents a connection on a fibered manifold.
Treating a connection as a vertical-valued form, one comes to the following important construction. Given a fibered manifold 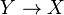 , let
, let 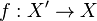 be a morphism and
be a morphism and 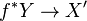 the pullback bundle of
the pullback bundle of  by
by  . Then any connection
. Then any connection 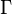 (3) on
(3) on 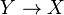 induces the pullback connection
induces the pullback connection
on 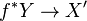 .
.
Connection as a jet bundle section
Let 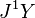 be the jet manifold of sections of a fibered manifold
be the jet manifold of sections of a fibered manifold 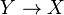 , with coordinates
, with coordinates 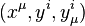 . Due to the canonical imbedding
. Due to the canonical imbedding
any connection 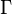 (3) on a fibered manifold
(3) on a fibered manifold  is represented by a global section
is represented by a global section
of the jet bundle 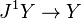 , and vice versa. It is an affine bundle modelled on a vector bundle
, and vice versa. It is an affine bundle modelled on a vector bundle
There are the following corollaries of this fact.
(i) Connections on a fibered manifold 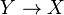 make up an affine space modelled on the vector space of soldering forms
make up an affine space modelled on the vector space of soldering forms
on 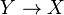 , i.e., sections of the vector bundle (4).
, i.e., sections of the vector bundle (4).
(ii) Connection coefficients possess the coordinate transformation law
(iii) Every connection 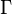 on a fibred manifold
on a fibred manifold 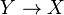 yields the first order differential operator
yields the first order differential operator
on  called the covariant differential relative to the connection
called the covariant differential relative to the connection 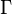 . If
. If 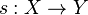 is a section, its covariant differential
is a section, its covariant differential
and the covariant derivative 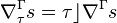 along a vector field
along a vector field 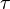 on
on  are defined.
are defined.
Curvature and torsion
Given the connection 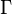 (3) on a fibered manifold
(3) on a fibered manifold 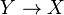 , its curvature is defined as the Nijenhuis differential
, its curvature is defined as the Nijenhuis differential
This is a vertical-valued horizontal two-form on  .
.
Given the connection 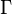 (3) and the soldering form
(3) and the soldering form 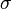 (5), a torsion of
(5), a torsion of 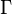 with respect to
with respect to 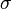 is defined as
is defined as
Bundle of principal connections
Let 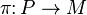 be a principal bundle with a structure Lie group
be a principal bundle with a structure Lie group  . A principal connection on
. A principal connection on  usually is described by a Lie algebra-valued connection one-form on
usually is described by a Lie algebra-valued connection one-form on  . At the same time, a principal connection on
. At the same time, a principal connection on  is a global section of the jet bundle
is a global section of the jet bundle 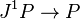 which is equivariant with respect to the canonical right action of
which is equivariant with respect to the canonical right action of  in
in  . Therefore, it is represented by a global section of the quotient bundle
. Therefore, it is represented by a global section of the quotient bundle 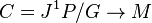 , called the bundle of principal connections. It is an affine bundle modelled on the vector bundle
, called the bundle of principal connections. It is an affine bundle modelled on the vector bundle 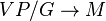 whose typical fiber is the Lie algebra
whose typical fiber is the Lie algebra 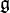 of structure group
of structure group  , and where
, and where  acts on by the adjoint representation. There is the canonical imbedding of
acts on by the adjoint representation. There is the canonical imbedding of  to the quotient bundle
to the quotient bundle 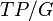 which also is called the bundle of principal connections.
which also is called the bundle of principal connections.
Given a basis 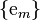 for a Lie algebra of
for a Lie algebra of  , the fiber bundle
, the fiber bundle  is endowed with bundle coordinates
is endowed with bundle coordinates 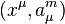 , and its sections are represented by vector-valued one-forms
, and its sections are represented by vector-valued one-forms
where 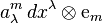 are the familiar local connection forms on
are the familiar local connection forms on 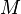 .
.
Let us note that the jet bundle 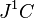 of
of  is a configuration space of Yang–Mills gauge theory. It admits the canonical decomposition
is a configuration space of Yang–Mills gauge theory. It admits the canonical decomposition
where
is called the strength form of a principal connection.
See also
Notes
References
- Kolář, Ivan; Michor, Peter; Slovák, Jan (1993), Natural operators in differential geometry (PDF), Springer-Verlag
- Krupka, Demeter; Janyška, Josef (1990), Lectures on differential invariants, Univerzita J. E. Purkyně V Brně, ISBN 80-210-0165-8
- Saunders, D.J. (1989), The geometry of jet bundles, Cambridge University Press, ISBN 0-521-36948-7
- Mangiarotti, L., Sardanashvily, G., Connections in Classical and Quantum Field Theory. World Scientific, 2000. ISBN 981-02-2013-8.
External links
- Sardanashvily, G., Advanced Differential Geometry for Theoreticians. Fiber bundles, jet manifolds and Lagrangian theory, Lambert Academic Publishing, 2013. ISBN 978-3-659-37815-7; arXiv: 0908.1886
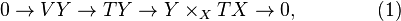
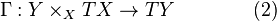
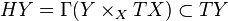
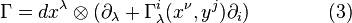
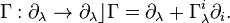
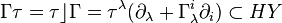
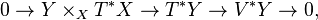
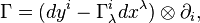
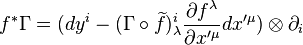
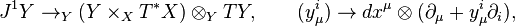

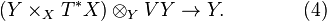
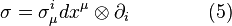
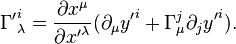
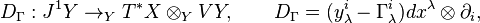
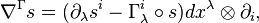
![R=\frac{1}{2} d_\Gamma\Gamma=\frac{1}{2} [\Gamma,\Gamma]_{FN} = \frac12 R_{\lambda\mu}^i \, dx^\lambda\wedge dx^\mu\otimes\partial_i,](../I/m/c3527fd62f003e20e932fe7089b27251.png)