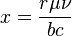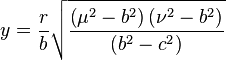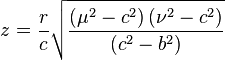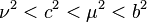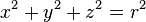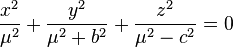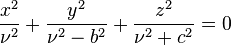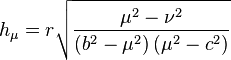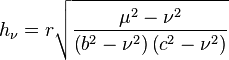Conical coordinates

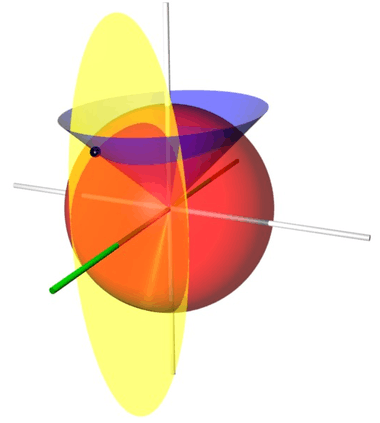
Coordinate surfaces of the conical coordinates. The constants b and c were chosen as 1 and 2, respectively. The red sphere represents r=2, the blue elliptic cone aligned with the vertical z-axis represents μ=cosh(1) and the yellow elliptic cone aligned with the (green) x-axis corresponds to ν² = 2/3. The three surfaces intersect at the point P (shown as a black sphere) with Cartesian coordinates roughly (1.26, -0.78, 1.34). The elliptic cones intersect the sphere in taco-shaped curves.

Conical coordinates are a three-dimensional orthogonal coordinate system consisting of concentric spheres (described by their radius $r$ ) and by two families of perpendicular cones, aligned along the z- and x-axes, respectively.

Basic definitions

The conical coordinates 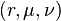$(r, \mu, \nu)$ are defined by

x = \frac{r\mu\nu}{bc}

y = \frac{r}{b} \sqrt{\frac{\left( \mu^{2} - b^{2} \right) \left( \nu^{2} - b^{2} \right)}{\left( b^{2} - c^{2} \right)} }

z = \frac{r}{c} \sqrt{\frac{\left( \mu^{2} - c^{2} \right) \left( \nu^{2} - c^{2} \right)}{\left( c^{2} - b^{2} \right)} }

with the following limitations on the coordinates

\nu^{2} < c^{2} < \mu^{2} < b^{2}

Surfaces of constant $r$ are spheres of that radius centered on the origin

x^{2} + y^{2} + z^{2} = r^{2}

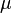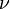whereas surfaces of constant $\mu$ and $\nu$ are mutually perpendicular cones

\frac{x^{2}}{\mu^{2}} + \frac{y^{2}}{\mu^{2} + b^{2}} + \frac{z^{2}}{\mu^{2} - c^{2}} = 0

\frac{x^{2}}{\nu^{2}} + \frac{y^{2}}{\nu^{2} - b^{2}} + \frac{z^{2}}{\nu^{2} + c^{2}} = 0

In this coordinate system, both Laplace's equation and the Helmholtz equation are separable.

Scale factors

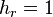The scale factor for the radius $r$ is one ( $h_{r} = 1$ ), as in spherical coordinates. The scale factors for the two conical coordinates are

h_{\mu} = r \sqrt{\frac{\mu^{2} - \nu^{2}}{\left( b^{2} - \mu^{2} \right) \left( \mu^{2} - c^{2} \right)}}

h_{\nu} = r \sqrt{\frac{\mu^{2} - \nu^{2}}{\left( b^{2} - \nu^{2} \right) \left( c^{2} - \nu^{2} \right)}}

References

Bibliography

Morse PM, Feshbach H (1953). Methods of Theoretical Physics, Part I. New York: McGraw-Hill. p. 659. ISBN 0-07-043316-X. LCCN 52011515.
Margenau H, Murphy GM (1956). The Mathematics of Physics and Chemistry. New York: D. van Nostrand. pp. 183–184. LCCN 55010911.
Korn GA, Korn TM (1961). Mathematical Handbook for Scientists and Engineers. New York: McGraw-Hill. p. 179. LCCN 59014456. ASIN B0000CKZX7.
Sauer R, Szabó I (1967). Mathematische Hilfsmittel des Ingenieurs. New York: Springer Verlag. pp. 991–100. LCCN 67025285.
Arfken G (1970). Mathematical Methods for Physicists (2nd ed.). Orlando, FL: Academic Press. pp. 118–119. ASIN B000MBRNX4.
Moon P, Spencer DE (1988). "Conical Coordinates (r, θ, λ)". Field Theory Handbook, Including Coordinate Systems, Differential Equations, and Their Solutions (corrected 2nd ed., 3rd print ed.). New York: Springer-Verlag. pp. 37–40 (Table 1.09). ISBN 978-0-387-18430-2.

External links

MathWorld description of conical coordinates

Orthogonal coordinate systems

Two dimensional	Cartesian coordinate system Polar coordinate system Parabolic coordinate system Bipolar coordinates Elliptic coordinates

Three dimensional	Cartesian coordinate system Cylindrical coordinate system Spherical coordinate system Parabolic cylindrical coordinates Paraboloidal coordinates Oblate spheroidal coordinates Prolate spheroidal coordinates Ellipsoidal coordinates Elliptic cylindrical coordinates Toroidal coordinates Bispherical coordinates Bipolar cylindrical coordinates Conical coordinates 6-sphere coordinates Flat-ring cyclide coordinates Flat-disk cyclide coordinates Bi-cyclide coordinates Cap-cyclide coordinates Concave bi-sinusoidal single-centered coordinates Concave bi-sinusoidal double-centered coordinates Convex inverted-sinusoidal spherically aligned coordinates Quasi-random-intersection cartesian coordinates