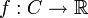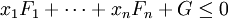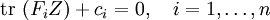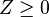Conic optimization
Conic optimization is a subfield of convex optimization that studies a class of structured convex optimization problems called conic optimization problems. A conic optimization problem consists of minimizing a convex function over the intersection of an affine subspace and a convex cone.
The class of conic optimization problems is a subclass of convex optimization problems and it includes some of the most well known classes of convex optimization problems, namely linear and semidefinite programming.
Definition
Given a real vector space X, a convex, real-valued function
defined on a convex cone 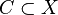 , and an affine subspace
, and an affine subspace  defined by a set of affine constraints
defined by a set of affine constraints 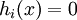 , a conic optimization problem is to find the point
, a conic optimization problem is to find the point  in
in 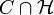 for which the number
for which the number 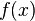 is smallest. Examples of
is smallest. Examples of  include the positive semidefinite matrices
include the positive semidefinite matrices 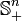 , the positive orthant
, the positive orthant 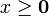 for
for 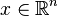 , and the second-order cone
, and the second-order cone 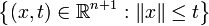 . Often
. Often 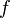 is a linear function, in which case the conic optimization problem reduces to a semidefinite program, a linear program, and a second order cone program, respectively.
is a linear function, in which case the conic optimization problem reduces to a semidefinite program, a linear program, and a second order cone program, respectively.
Duality
Certain special cases of conic optimization problems have notable closed-form expressions of their dual problems.
Conic LP
The dual of the conic linear program
- minimize
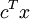
- subject to
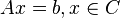
is
- maximize
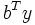
- subject to
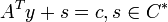
where 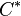 denotes the dual cone of
denotes the dual cone of 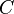 .
.
Semidefinite Program
The dual of a semidefinite program in inequality form,
minimize 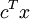 subject to
subject to
is given by
maximize 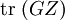 subject to
subject to
External links
- Boyd, Stephen P.; Vandenberghe, Lieven (2004). Convex Optimization (pdf). Cambridge University Press. ISBN 978-0-521-83378-3. Retrieved October 15, 2011.
- MOSEK Software capable of solving conic optimization problems.