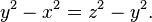Congruum
In number theory, a congruum (plural congrua) is the difference between successive square numbers in an arithmetic progression of three squares. That is, if x2, y2, and z2 (for integers x, y, and z) are three square numbers that are equally spaced apart from each other, then the spacing between them, z2 − y2 = y2 − x2, is called a congruum.
The congruum problem is the problem of finding squares in arithmetic progression and their associated congrua.[1] It can be formalized as a Diophantine equation: find integers x, y, and z such that
When this equation is satisfied, both sides of the equation equal the congruum.
Fibonacci solved the congruum problem by finding a parameterized formula for generating all congrua, together with their associated arithmetic progressions. According to this formula, each congruum is four times the area of a Pythagorean triangle. Congrua are also closely connected with congruent numbers: every congruum is a congruent number, and every congruent number is a congruum multiplied by the square of a rational number.
Examples
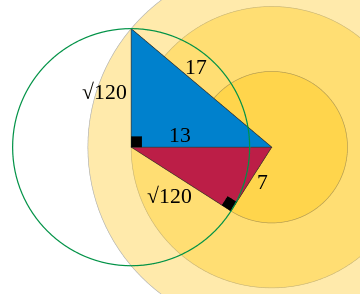
For instance, the number 96 is a congruum, since it is the difference between each pair of the three squares 4, 100, and 196 (the squares of 2, 10, and 14 respectively).
The first few congrua are:
History
The congruum problem was originally posed in 1225, as part of a mathematical tournament held by Frederick II, Holy Roman Emperor, and answered correctly at that time by Fibonacci, who recorded his work on this problem in his Book of Squares.[2]
Fibonacci was already aware that it is impossible for a congruum to itself be a square, but did not give a satisfactory proof of this fact.[3] Geometrically, this means that it is not possible for the pair of legs of a Pythagorean triangle to be the leg and hypotenuse of another Pythagorean triangle. A proof was eventually given by Pierre de Fermat, and the result is now known as Fermat's right triangle theorem. Fermat also conjectured, and Leonhard Euler proved, that there is no sequence of four squares in arithmetic progression.[4][5]
Parameterized solution
The congruum problem may be solved by choosing two distinct positive integers m and n (with m > n); then the number 4mn(m2 −n2) is a congruum. The middle square of the associated arithmetic progression of squares is (m2 + n2)2, and the other two squares may be found by adding or subtracting the congruum. All solutions arise in this way.[1] For instance, the congruum 96 can be constructed by these formulas with m = 3 and n = 1.
An equivalent formulation of this solution, given by Bernard Frénicle de Bessy, is that for the three squares in arithmetic progression x2, y2, and z2, the middle number y is the hypotenuse of a Pythagorean triangle and the other two numbers x and z are the difference and sum respectively of the triangle's two sides.[6] The congruum itself is four times the area of the same Pythagorean triangle. The example of an arithmetic progression with the congruum 96 can be obtained in this way from a right triangle with side and hypotenuse lengths 6, 8, and 10.
Relation to congruent numbers
A congruent number is defined as the area of a right triangle with rational sides. Because every congruum can be obtained (using the parameterized solution) as the area of a Pythagorean triangle, it follows that every congruum is congruent. Conversely, every congruent number is a congruum multiplied by the square of a rational number.[7] However, testing whether a number is a congruum is much easier than testing whether a number is congruent. For the congruum problem, the parameterized solution reduces this testing problem to checking a finite set of parameter values. In contrast, for the congruent number problem, a finite testing procedure is known only conjecturally, via Tunnell's theorem, under the assumption that the Birch and Swinnerton-Dyer conjecture is true.[8]
See also
- Spiral of Theodorus, formed by right triangles whose (non-integer) sides, when squared, form an infinite arithmetic progression
References
- ↑ 1.0 1.1 Darling, David (2004), The Universal Book of Mathematics: From Abracadabra to Zeno's Paradoxes, John Wiley & Sons, p. 77, ISBN 978-0-471-66700-1.
- ↑ Bradley, Michael John (2006), The Birth of Mathematics: Ancient Times to 1300, Infobase Publishing, p. 124, ISBN 978-0-8160-5423-7.
- ↑ Ore, Øystein (2012), Number Theory and Its History, Courier Dover Corporation, pp. 202–203, ISBN 978-0-486-13643-1.
- ↑ Erickson, Martin J. (2011), Beautiful Mathematics, MAA Spectrum, Mathematical Association of America, pp. 94–95, ISBN 978-0-88385-576-8.
- ↑ Euler's proof is not clearly written. An elementary proof is given in Brown, Kevin, "No Four Squares In Arithmetic Progression", MathPages, retrieved 2014-12-06.
- ↑ Beiler, Albert H. (1964), Recreations in the Theory of Numbers: The Queen of Mathematics Entertains, Courier Corporation, p. 153, ISBN 978-0-486-21096-4.
- ↑ Conrad, Keith (Fall 2008), "The congruent number problem", Harvard College Mathematical Review 2 (2): 58–73.
- ↑ Koblitz, Neal (1984), Introduction to Elliptic Curves and Modular Forms, Graduate Texts in Mathematics, no. 97, Springer-Verlag, ISBN 0-387-97966-2