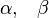Configuration state function
In quantum chemistry, a configuration state function (CSF), is a symmetry-adapted linear combination of Slater determinants. A CSF must not be confused with a configuration. In general, one configuration gives rise to several CSFs; all have the same total quantum numbers for spin and spatial parts but differ in their intermediate couplings.
Definition
In quantum chemistry, a configuration state function (CSF), is a symmetry-adapted linear combination of Slater determinants. It is constructed to have the same quantum numbers as the wavefunction, 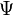 , of the system being studied. In the method of configuration interaction the wavefunction[1] can be expressed as a linear combination of CSFs, that is in the form
, of the system being studied. In the method of configuration interaction the wavefunction[1] can be expressed as a linear combination of CSFs, that is in the form
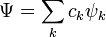
where 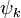 denotes the set of CSFs. The coefficients,
denotes the set of CSFs. The coefficients, 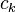 , are found by using the expansion of
, are found by using the expansion of 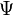 to compute a Hamiltonian matrix. When this is diagonalized, the eigenvectors are chosen as the expansion coefficients. CSFs rather than just Slater determinants can also be used as a basis in Multi-configurational self-consistent field computations.
to compute a Hamiltonian matrix. When this is diagonalized, the eigenvectors are chosen as the expansion coefficients. CSFs rather than just Slater determinants can also be used as a basis in Multi-configurational self-consistent field computations.
In atomic structure, a CSF is an eigenstate of
- the square of the angular momentum operator,
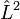 .
. - the z-projection of angular momentum
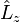
- the square of the spin operator
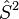 .
. - the z-projection of the spin operator
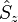
In linear molecules, 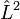 does not commute with the Hamiltonian for the system and therefore CSFs are not eigenstates of
does not commute with the Hamiltonian for the system and therefore CSFs are not eigenstates of 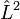 . However, the z-projection of angular momentum is still a good quantum number and CSFs are constructed to be eigenstates of
. However, the z-projection of angular momentum is still a good quantum number and CSFs are constructed to be eigenstates of 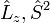 and
and 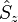 . In non-linear (which implies polyatomic) molecules, neither
. In non-linear (which implies polyatomic) molecules, neither 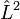 nor
nor 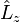 commute with the Hamiltonian. The CSFs are constructed to have the spatial transformation properties of one of the irreducible representations of the point group to which the nuclear framework belongs. This is because the Hamiltonian operator transforms in the same way.[2]
commute with the Hamiltonian. The CSFs are constructed to have the spatial transformation properties of one of the irreducible representations of the point group to which the nuclear framework belongs. This is because the Hamiltonian operator transforms in the same way.[2] 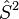 and
and 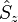 are still valid quantum numbers and CSFs are built to be eigenfunctions of these operators.
are still valid quantum numbers and CSFs are built to be eigenfunctions of these operators.
From Configurations to Configuration State Functions
CSFs are however derived from configurations. A configuration is just an assignment of electrons to orbitals. For example 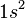 and
and 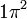 are example of two configurations, one from atomic structure and one from molecular structure.
are example of two configurations, one from atomic structure and one from molecular structure.
From any given configuration we can, in general, create several CSFs. CSFs are therefore sometimes also called N-particle symmetry adapted basis functions. It is important to realize that for a configuration the number of electrons is fixed; let's call this  . When we are creating CSFs from a configuration we have to work with the spin-orbitals associated with the configuration.
. When we are creating CSFs from a configuration we have to work with the spin-orbitals associated with the configuration.
For example given the 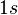 orbital in an atom we know that there are two spin-orbitals associated with this,
orbital in an atom we know that there are two spin-orbitals associated with this,
where
are the one electron spin-eigenfunctions for spin-up and spin-down respectively. Similarly, for the 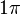 orbital in a linear molecule (
orbital in a linear molecule (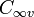 point group) we have four spin orbitals:
point group) we have four spin orbitals:
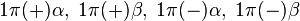 .
.
This is because the 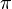 designation corresponds to z-projection of angular momentum of both
designation corresponds to z-projection of angular momentum of both 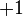 and
and 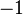 .
.
We can think of the set of spin orbitals as a set of boxes each of size one; let's call this  boxes. We distribute the
boxes. We distribute the  electrons among the
electrons among the  boxes in all possible ways. Each assignment corresponds to one Slater determinant,
boxes in all possible ways. Each assignment corresponds to one Slater determinant, 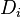 . There can be great number of these, particularly when
. There can be great number of these, particularly when 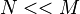 . Another way to look at this is to say we have
. Another way to look at this is to say we have  entities and we wish to select
entities and we wish to select  of them, known as a combination. We need to find all possible combinations. Order of the selection is not significant because we are working with determinants and can interchange rows as required.
of them, known as a combination. We need to find all possible combinations. Order of the selection is not significant because we are working with determinants and can interchange rows as required.
If we then specify the overall coupling that we wish to achieve for the configuration, we can now select only those Slater determinants that have the required quantum numbers. In order to achieve the required total spin angular momentum (and in the case of atoms the total orbital angular momentum as well), each Slater determinant has to be premultiplied by a coupling coefficient 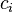 , derived ultimately from Clebsch–Gordan coefficients. Thus the CSF is a linear combination
, derived ultimately from Clebsch–Gordan coefficients. Thus the CSF is a linear combination
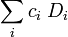 .
.
The Lowdin projection operator formalism[3] may be used to find the coefficients. For any given set of determinants 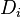 it may be possible to find several different sets of coefficients.[4] Each set corresponds to one CSF. In fact this simply reflects the different internal couplings of total spin and spatial angular momentum.
it may be possible to find several different sets of coefficients.[4] Each set corresponds to one CSF. In fact this simply reflects the different internal couplings of total spin and spatial angular momentum.
A genealogical algorithm for CSF construction
At the most fundamental level, a configuration state function can be constructed
- from a set of
 orbitals
orbitals
and
- a number
 of electrons
of electrons
using the following genealogical algorithm:
- distribute the
 electrons over the set of
electrons over the set of  orbitals giving a configuration
orbitals giving a configuration - for each orbital the possible quantum number couplings (and therefore wavefunctions for the individual orbitals) are known from basic quantum mechanics; for each orbital choose one of the permitted couplings but leave the z-component of the total spin,
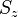 undefined.
undefined. - check that the spatial coupling of all orbitals matches that required for the system wavefunction. For a molecule exhibiting
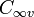 or
or 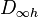 this is achieved by a simple linear summation of the coupled
this is achieved by a simple linear summation of the coupled  value for each orbital; for molecules whose nuclear framework transforms according to
value for each orbital; for molecules whose nuclear framework transforms according to 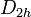 symmetry, or one of its sub-groups, the group product table has to be used to find the product of the irreducible representation of all
symmetry, or one of its sub-groups, the group product table has to be used to find the product of the irreducible representation of all  orbitals.
orbitals. - couple the total spins of the
 orbitals from left to right; this means we have to choose a fixed
orbitals from left to right; this means we have to choose a fixed 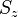 for each orbital.
for each orbital. - test the final total spin and its z-projection against the values required for the system wavefunction
The above steps will need to be repeated many times to elucidate the total set of CSFs that can be derived from
the  electrons and
electrons and  orbitals.
orbitals.
Single Orbital configurations and wavefunctions
Basic quantum mechanics defines the possible single orbital wavefunctions. In a software implementation, these can be provided either as a table or through a set of logic statements. Alternatively group theory may be used to compute them [5] Electrons in a single orbital are called equivalent electrons. [6] They obey the same coupling rules as other electrons but the Pauli exclusion principle makes certain couplings impossible. The Pauli exclusion principle requires that no two electrons in a system can have all their quantum numbers equal. For equivalent electrons, by definition the principal quantum number is identical. In atoms the angular momentum is also identical. So, for equivalent electrons the z components of spin and spatial parts, taken together, must differ.
The following table shows the possible couplings for a  orbital with one or two electrons.
orbital with one or two electrons.
| Orbital Configuration | Term symbol | 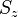 projection projection |
|---|---|---|
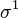 |
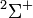 |
 |
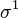 |
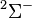 |
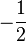 |
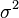 |
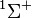 |
 |
The situation for orbitals in Abelian point groups mirrors the above table. The next table shows the fifteen possible couplings for a 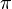 orbital.
The
orbital.
The 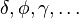 orbitals also each generate fifteen possible
couplings, all of which can be easily inferred from this table.
orbitals also each generate fifteen possible
couplings, all of which can be easily inferred from this table.
| Orbital Configuration | Term symbol | Lambda coupling | 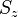 projection projection |
|---|---|---|---|
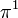 |
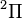 |
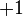 |
 |
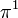 |
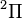 |
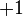 |
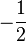 |
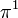 |
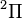 |
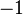 |
 |
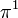 |
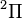 |
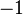 |
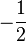 |
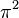 |
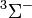 |
 |
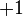 |
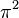 |
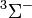 |
 |
 |
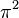 |
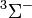 |
 |
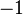 |
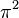 |
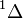 |
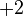 |
 |
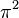 |
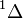 |
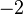 |
 |
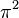 |
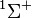 |
 |
 |
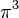 |
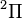 |
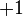 |
 |
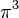 |
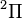 |
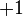 |
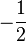 |
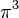 |
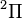 |
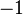 |
 |
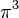 |
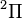 |
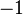 |
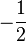 |
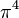 |
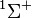 |
 |
 |
Similar tables can be constructed for atomic systems, which transform according to the point group of the sphere,
that is for s, p, d, f 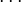 orbitals. The number of term sysmbols and therefore possible couplings
is significantly larger in the atomic case.
orbitals. The number of term sysmbols and therefore possible couplings
is significantly larger in the atomic case.
Computer Software for CSF generation
Computer programs are readily available to generate CSFs for atoms[7] for molecules [8] and for electron and positron scattering by molecules .[9] A popular computational method for CSF construction is the Graphical Unitary Group Approach.
References
- ↑ Engel, T. (2006). Quantum Chemistry and Spectroscopy. Pearson PLC. ISBN 0-8053-3842-X.
- ↑ Pilar, F. L. (1990). Elementary Quantum Chemistry (2nd ed.). Dover Publications. ISBN 0-486-41464-7.
- ↑ Crossley, R. J. S. (1977). "On Löwdin's projection operators for angular momentum. I". International Journal of Quantum Chemistry 11 (6): 917–929. doi:10.1002/qua.560110605.
- ↑ Nesbet, R. K. (2003). "Section 4.4". In Huo; Gianturco, F. A. Variational principles and methods in theoretical physics and chemistry. Cambridge University Press. p. 49. ISBN 0-521-80391-8.
- ↑ Karayianis, N. (1965). "Atomic Term Symbols for Equivalent Electrons". J. Math. Phys. 6: 1204. Bibcode:1965JMP.....6.1204K. doi:10.1063/1.1704761.
- ↑ Wise, J.H. (1976). "Spectroscopic terms for equivalent electrons". J. Chem. Educ. 53 (8): 496. Bibcode:1976JChEd..53..496W. doi:10.1021/ed053p496.2.
- ↑ Sturesson, L.; Fischer, C. F. (1993). "LSGEN - a program to generate configuration-state lists of LS-coupled basis functions". Computer Physics Communications 74 (3): 432–440. Bibcode:1993CoPhC..74..432S. doi:10.1016/0010-4655(93)90024-7.
- ↑ McLean, A. D. et al. (1991). "ALCHEMY II, A Research Tool for Molecular Electronic Structure and Interactions". In Clementi, E. Modern Techniques in Computational Chemistry (MOTECC-91). ESCOM Science Publishers. ISBN 90-72199-10-3.
- ↑ Morgan, L. A.; Tennyson, J.; Gillan, C. J. (1998). "The UK molecular R-matrix codes". Computer Physics Communications 114 (1–3): 120–128. Bibcode:1998CoPhC.114..120M. doi:10.1016/S0010-4655(98)00056-3.