Cone of curves
In mathematics, the cone of curves (sometimes the Kleiman-Mori cone) of an algebraic variety  is a combinatorial invariant of much importance to the birational geometry of
is a combinatorial invariant of much importance to the birational geometry of  .
.
Definition
Let  be a proper variety. By definition, a (real) 1-cycle on
be a proper variety. By definition, a (real) 1-cycle on  is a formal linear combination
is a formal linear combination 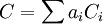 of irreducible, reduced and proper curves
of irreducible, reduced and proper curves 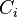 , with coefficients
, with coefficients 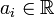 . Numerical equivalence of 1-cycles is defined by intersections: two 1-cycles
. Numerical equivalence of 1-cycles is defined by intersections: two 1-cycles  and
and 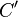 are numerically equivalent if
are numerically equivalent if 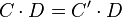 for every Cartier divisor
for every Cartier divisor  on
on  . Denote the real vector space of 1-cycles modulo numerical equivalence by
. Denote the real vector space of 1-cycles modulo numerical equivalence by 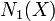 .
.
We define the cone of curves of  to be
to be
where the 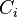 are irreducible, reduced, proper curves on
are irreducible, reduced, proper curves on  , and
, and ![[C_i]](../I/m/44f392fad32357883e9c1c59912ef931.png) their classes in
their classes in 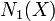 . It is not difficult to see that
. It is not difficult to see that 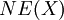 is indeed a convex cone in the sense of convex geometry.
is indeed a convex cone in the sense of convex geometry.
Applications
One useful application of the notion of the cone of curves is the Kleiman condition, which says that a (Cartier) divisor  on a complete variety
on a complete variety  is ample if and only if
is ample if and only if 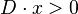 for any nonzero element
for any nonzero element  in
in 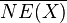 , the closure of the cone of curves in the usual real topology. (In general,
, the closure of the cone of curves in the usual real topology. (In general, 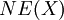 need not be closed, so taking the closure here is important.)
need not be closed, so taking the closure here is important.)
A more involved example is the role played by the cone of curves in the theory of minimal models of algebraic varieties. Briefly, the goal of that theory is as follows: given a (mildly singular) projective variety  , find a (mildly singular) variety
, find a (mildly singular) variety 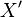 which is birational to
which is birational to  , and whose canonical divisor
, and whose canonical divisor 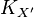 is nef. The great breakthrough of the early 1980s (due to Mori and others) was to construct (at least morally) the necessary birational map from
is nef. The great breakthrough of the early 1980s (due to Mori and others) was to construct (at least morally) the necessary birational map from  to
to 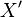 as a sequence of steps, each of which can be thought of as contraction of a
as a sequence of steps, each of which can be thought of as contraction of a 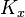 -negative extremal ray of
-negative extremal ray of 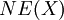 . This process encounters difficulties, however, whose resolution necessitates the introduction of the flip.
. This process encounters difficulties, however, whose resolution necessitates the introduction of the flip.
A structure theorem
The above process of contractions could not proceed without the fundamental result on the structure of the cone of curves known as the Cone Theorem. The first version of this theorem, for smooth varieties, is due to Mori; it was later generalised to a larger class of varieties by Kollár, Reid, Shokurov, and others. Mori's version of the theorem is as follows:
Cone Theorem. Let  be a smooth projective variety. Then
be a smooth projective variety. Then
1. There are countably many rational curves 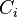 on
on  , satisfying
, satisfying 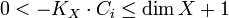 , and
, and
2. For any positive real number  and any ample divisor
and any ample divisor  ,
,
where the sum in the last term is finite.
The first assertion says that, in the closed half-space of 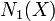 where intersection with
where intersection with 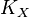 is nonnegative, we know nothing, but in the complementary half-space, the cone is spanned by some countable collection of curves which are quite special: they are rational, and their 'degree' is bounded very tightly by the dimension of
is nonnegative, we know nothing, but in the complementary half-space, the cone is spanned by some countable collection of curves which are quite special: they are rational, and their 'degree' is bounded very tightly by the dimension of  . The second assertion then tells us more: it says that, away from the hyperplane
. The second assertion then tells us more: it says that, away from the hyperplane 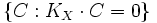 , extremal rays of the cone cannot accumulate.
, extremal rays of the cone cannot accumulate.
If in addition the variety  is defined over a field of characteristic 0, we have the following assertion, sometimes referred to as the Contraction Theorem:
is defined over a field of characteristic 0, we have the following assertion, sometimes referred to as the Contraction Theorem:
3. Let 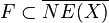 be an extremal face of the cone of curves on which
be an extremal face of the cone of curves on which 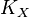 is negative. Then there is a unique morphism
is negative. Then there is a unique morphism 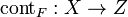 to a projective variety Z, such that
to a projective variety Z, such that 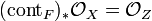 and an irreducible curve
and an irreducible curve  in
in  is mapped to a point by
is mapped to a point by 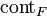 if and only if
if and only if ![[C] \in F](../I/m/fcdae7d80bfee730f69e7ac2607da256.png) .
.
References
- Lazarsfeld, R., Positivity in Algebraic Geometry I, Springer-Verlag, 2004. ISBN 3-540-22533-1
- Kollár, J. and Mori, S., Birational Geometry of Algebraic Varieties, Cambridge University Press, 1998. ISBN 0-521-63277-3
![NE(X) = \left\{\sum a_i[C_i], \ 0 \leq a_i \in \mathbb{R} \right\}](../I/m/74d9ade875842fe21645881ce2afd655.png)
![\overline{NE(X)} = \overline{NE(X)}_{K_X\geq 0} + \sum_i \mathbf{R}_{\geq0} [C_i].](../I/m/78bb9a726d16ca12b5263d733333926f.png)
![\overline{NE(X)} = \overline{NE(X)}_{K_X+\epsilon H\geq0} + \sum \mathbf{R}_{\geq0} [C_i],](../I/m/3f517c29621e8403a456eb92b50902e5.png)