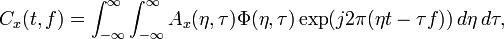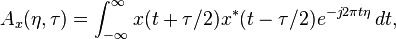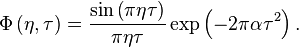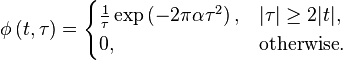Cone-shape distribution function

In mathematics, cone-shape distribution function is one of the members of Cohen's class distribution function. It was first proposed by Yunxin Zhao, Les E. Atlas, and Robert J. Marks in 1990. The reason why this distribution is so named is because its kernel function in 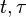t, \tau domain looks like two cones. The advantage of this special kernel function is that it can completely remove the cross-term between two components that have same center frequency, but on the other hand, the cross-term results from components with the same time center cannot be completely removed by the cone-shaped kernel.

Mathematical definition

The definition of the cone-shape distribution function is shown as follows:

C_x(t, f)=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}A_x(\eta,\tau)\Phi(\eta,\tau)\exp (j2\pi(\eta t-\tau f))\, d\eta\, d\tau,

where

A_x(\eta,\tau)=\int_{-\infty}^{\infty}x(t+\tau /2)x^*(t-\tau /2)e^{-j2\pi t\eta}\, dt,

and the kernel function is

\Phi \left(\eta,\tau \right) = \frac{\sin \left(\pi \eta \tau \right)}{ \pi \eta \tau }\exp \left(-2\pi \alpha \tau^2 \right).

The kernel function in 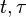t, \tau domain is defined as:

\phi \left(t,\tau \right) = \begin{cases} \frac{1}{\tau} \exp \left(-2\pi \alpha \tau^2 \right), & |\tau | \ge 2|t|, \\ 0, & \mbox{otherwise}. \end{cases}

Following are the magnitude distribution of the kernel function in 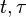t, \tau domain.

Following are the magnitude distribution of the kernel function in 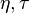\eta, \tau domain with different \alpha values.

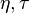As we can see from the figure above, a properly chosen kernel of cone-shape distribution function can filter out the interference on the \tau axis in the \eta, \tau domain, or the ambiguity domain. Therefore, unlike the Choi-Williams distribution function, the cone-shape distribution function can effectively reduce the cross-term results form two component with same center frequency. However, the cross-terms on the 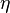\eta axis are still preserved.

See also

References

External links