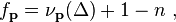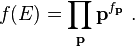Conductor of an elliptic curve

In mathematics, the conductor of an elliptic curve over the field of rational numbers, or more generally a local or global field, is an integral ideal analogous to the Artin conductor of a Galois representation. It is given as a product of prime ideals, together with associated exponents, which encode the ramification in the field extensions generated by the points of finite order in the group law of the elliptic curve. The primes involved in the conductor are precisely the primes of bad reduction of the curve: this is the Néron–Ogg–Shafarevich criterion.

Ogg's formula expresses the conductor in terms of the discriminant and the number of components of the special fiber over a local field, which can be computed using Tate's algorithm.

History

The conductor of an elliptic curve over a local field was implicitly studied (but not named) by Ogg (1967) in the form of an integer invariant ε+δ which later turned out to be the exponent of the conductor.

The conductor of an elliptic curve over the rationals was introduced and named by Weil (1967) as a constant appearing in the functional equation of its L-series, analogous to the way the conductor of a global field appears in the functional equation of its zeta function. He showed that it could be written as a product over primes with exponents given by order(Δ) − μ + 1, which by Ogg's formula is equal to ε+δ. A similar definitionworks for any global field. Weil also suggested that the conductor was equal to the level of a modular form corresponding to the elliptic curve.

Serre & Tate (1968) extended the theory to conductors of abelian varieties.

Definition

Let E be an elliptic curve defined over a local field K and p the prime ideal of the ring of integers of K. We consider a minimal equation for E: a generalised Weierstrass equation whose coeficients are p-integral and with the valuation of the discriminant νp(Δ) as small as possible. If the discriminant is a p-unit then E has good reduction at p and the exponent of the conductor is zero.

We can write the exponent f of the conductor as a sum ε + δ of 2 terms, corresponding to the tame and wild ramification. The tame ramification part ε is defined in terms of the reduction type: ε=0 for good reduction, ε=1 for multiplicative reduction and ε=2 for additive reduction. The wild ramification term δ is zero unless p divides 2 or 3, and in the latter cases it is defined in terms of the wild ramification of the extensions of K by the division points of E by Serre's formula

\delta = \dim_{Z/lZ} \text {Hom}_{Z_l[G]}(P, M).

Here M is the group of points on the elliptic curve of order l for a prime l, P is the Swan representation, and G the Galois group of a finite extension of K such that the points of M are defined over it (so that G acts on M)

Ogg's formula

The exponent of the conductor is related to other invariants of the elliptic curve by Ogg's formula:

f_\mathbf{p} = \nu_\mathbf{p} ( \Delta ) + 1 - n \ ,

where n is the number of components (without counting multiplicities) of the singular fibre of the Néron minimal model for E. (This is sometimes used as a definition of the conductor).

Ogg's original proof used a lot of case by case checking, especially in characteristics 2 and 3. Saito (1988) gave a uniform proof and generalized Ogg's formula to more general arithmetic surfaces.

We can also describe ε in terms of the valuation of the j-invariant νp(j): it is 0 in the case of good reduction; otherise it is 1 if νp(j) < 0 and 2 if νp(j) ≥ 0.

Global conductor

Let E be an elliptic curve defined over a number field K. The global conductor is the ideal given by the product over primes of K

f(E) = \prod_\mathbf{p} \mathbf{p}^{f_\mathbf{p}} \ .

This is a finite product as the primes of bad reduction are contained in the set of primes divisors of the discriminant of any model for E with global integral coefficients.

References

    External links