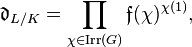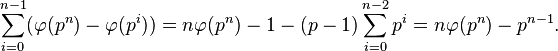Conductor-discriminant formula
In mathematics, the conductor-discriminant formula or Führerdiskriminantenproduktformel, introduced by Hasse (1926, 1930) for abelian extensions and by Artin (1931) for Galois extensions, is a formula calculating the relative discriminant of a finite Galois extension 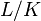 of local or global fields from the Artin conductors of the irreducible characters
of local or global fields from the Artin conductors of the irreducible characters 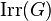 of the Galois group
of the Galois group 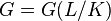 .
.
Statement
Let 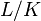 be a finite Galois extension of global fields with Galois group
be a finite Galois extension of global fields with Galois group  . Then the discriminant equals
. Then the discriminant equals
where 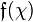 equals the global Artin conductor of
equals the global Artin conductor of 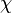 .[1]
.[1]
Example
Let 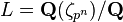 be a cyclotomic extension of the rationals. The Galois group
be a cyclotomic extension of the rationals. The Galois group  equals
equals 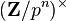 . Because
. Because 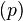 is the only finite prime ramified, the global Artin conductor
is the only finite prime ramified, the global Artin conductor 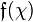 equals the local one
equals the local one 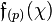 . Because
. Because  is abelian, every non-trivial irreducible character
is abelian, every non-trivial irreducible character 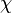 is of degree
is of degree 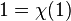 . Then, the local Artin conductor of
. Then, the local Artin conductor of 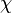 equals the conductor of the
equals the conductor of the 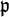 -adic completion of
-adic completion of 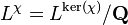 , i.e.
, i.e. 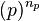 , where
, where 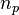 is the smallest natural number such that
is the smallest natural number such that 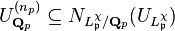 . If
. If 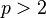 , the Galois group
, the Galois group 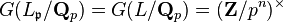 is cyclic of order
is cyclic of order 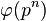 , and by local class field theory and using that
, and by local class field theory and using that 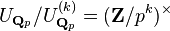 one sees easily that
one sees easily that 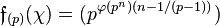 : the exponent is
: the exponent is
Notes
- ↑ Neukirch 1999, VII.11.9.
References
- Artin, Emil (1931), "Die gruppentheoretische Struktur der Diskriminanten algebraischer Zahlkörper.", Journal für Reine und Angewandte Mathematik (in German) 164: 1–11, doi:10.1515/crll.1931.164.1, ISSN 0075-4102, Zbl 0001.00801
- Hasse, H. (1926), "Bericht über neuere Untersuchungen und Probleme aus der Theorie der algebraischen Zahlkörper. I: Klassenkörpertheorie.", Jahresbericht der Deutschen Mathematiker-Vereinigung (in German) 35: 1–55
- Hasse, H. (1930), "Führer, Diskriminante und Verzweigungskörper relativ-Abelscher Zahlkörper.", Journal für die reine und angewandte Mathematik (in German) 162: 169–184, doi:10.1515/crll.1930.162.169, ISSN 0075-4102
- Neukirch, Jürgen (1999), Algebraic Number Theory, Grundlehren der mathematischen Wissenschaften 322, Berlin: Springer-Verlag, ISBN 978-3-540-65399-8, Zbl 0956.11021, MR 1697859