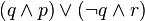Conditioned disjunction
In logic, conditioned disjunction (sometimes called conditional disjunction) is a ternary logical connective introduced by Church.[1] Given operands p, q, and r, which represent truth-valued propositions, the meaning of the conditioned disjunction [p, q, r] is given by:
![[p, q, r] ~\leftrightarrow~(q \rightarrow p) \and (\neg q \rightarrow r)](../I/m/6727eb8bfa2111fa22baa625c03101f0.png)
In words, [p, q, r] is equivalent to: "if q then p, else r", or "p or r, according as q or not q". This may also be stated as "q implies p and, not q implies r". So, for any values of p, q, and r, the value of [p, q, r] is the value of p when q is true, and is the value of r otherwise.
The conditioned disjunction is also equivalent to:
and has the same truth table as the "ternary" (?:) operator in many programming languages.
In conjunction with truth constants denoting each truth-value, conditioned disjunction is truth-functionally complete for classical logic.[2] Its truth table is the following:
| p | q | r | [p,q,r] |
|---|---|---|---|
| T | T | T | T |
| T | T | F | T |
| T | F | T | T |
| T | F | F | F |
| F | T | T | F |
| F | T | F | F |
| F | F | T | T |
| F | F | F | F |
There are other truth-functionally complete ternary connectives.
References
- ↑ Church, Alonzo (1956). Introduction to Mathematical Logic. Princeton University Press.
- ↑ Wesselkamper, T., "A sole sufficient operator", Notre Dame Journal of Formal Logic, Vol. XVI, No. 1 (1975), pp. 86-88.