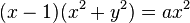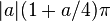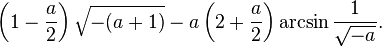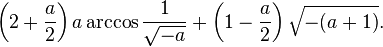Conchoid of de Sluze

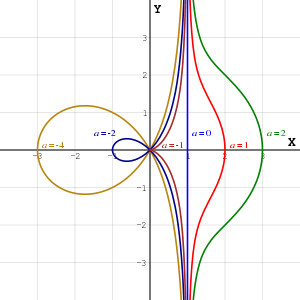
The Conchoid of de Sluze for several values of a

The conchoid(s) of de Sluze is a family of plane curves studied in 1662 by René François Walter, baron de Sluze.[1]

The curves are defined by the polar equation

r=\sec\theta+a\cos\theta \,.

In cartesian coordinates, the curves satisfy the implicit equation

(x-1)(x^2+y^2)=ax^2 \,

except that for a=0 the implicit form has an acnode (0,0) not present in polar form.

They are rational, circular, cubic plane curves.

These expressions have an asymptote x=1 (for a≠0). The point most distant from the asymptote is (1+a,0). (0,0) is a crunode for a<−1.

The area between the curve and the asymptote is, for 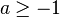a \ge -1,

|a|(1+a/4)\pi \,

while for 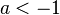a < -1, the area is

\left(1-\frac a2\right)\sqrt{-(a+1)}-a\left(2+\frac a2\right)\arcsin\frac1{\sqrt{-a}}.

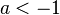If a<-1, the curve will have a loop. The area of the loop is

\left(2+\frac a2\right)a\arccos\frac1{\sqrt{-a}} + \left(1-\frac a2\right)\sqrt{-(a+1)}.

Four of the family have names of their own:

a=0, line (asymptote to the rest of the family)
a=−1, cissoid of Diocles
a=−2, right strophoid
a=−4, trisectrix of Maclaurin

References

  1. ↑ Smith, David Eugene (1958), History of Mathematics, Volume 2, Courier Dover Publications, p. 327, ISBN 9780486204307.