Concentration inequality
In mathematics, concentration inequalities provide probability bounds on how a random variable deviates from some value (e.g. its expectation). The laws of large numbers of classical probability theory state that sums of independent random variables are, under very mild conditions, close to their expectation with a large probability. Such sums are the most basic examples of random variables concentrated around their mean. Recent results shows that such behavior is shared by other functions of independent random variables.
Markov's inequality
If X is any random variable and a > 0, then
Proof can be found here.
We can extend Markov's inequality to a strictly increasing and non-negative function 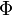 . We have
. We have
Chebyshev's inequality
Chebyshev's inequality is a special case of generalized Markov's inequality when 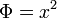
If X is any random variable and a > 0, then
Where Var(X) is the variance of X, defined as:
Asymptotic behavior of binomial distribution
If a random variable X follows the binomial distribution with parameter  and
and  . The probability of getting exact
. The probability of getting exact  successes in
successes in  trials is given by the probability mass function
trials is given by the probability mass function
Let 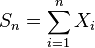 and
and  's are i.i.d. Bernoulli random variables with parameter
's are i.i.d. Bernoulli random variables with parameter  .
. 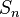 follows the binomial distribution with parameter
follows the binomial distribution with parameter  and
and  . Central Limit Theorem suggests when
. Central Limit Theorem suggests when 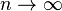 ,
, 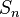 is approximately normally distributed with mean
is approximately normally distributed with mean 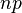 and variance
and variance 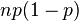 , and
, and
For 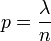 , where
, where  is a constant, the limit distribution of binomial distribution
is a constant, the limit distribution of binomial distribution 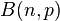 is the Poisson distribution
is the Poisson distribution 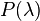
General Chernoff inequality
A Chernoff bound gives exponentially decreasing bounds on tail distributions of sums of independent random variables.[1] Let  denote independent but not necessarily identical random variables, satisfying
denote independent but not necessarily identical random variables, satisfying 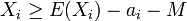 , for
, for 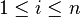 .
.
we have lower tail inequality:
If  satisfies
satisfies 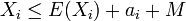 , we have upper tail inequality:
, we have upper tail inequality:
If  are i.i.d.,
are i.i.d., 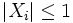 and
and 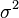 is the variance of
is the variance of  . A typical version of Chernoff Inequality is:
. A typical version of Chernoff Inequality is:
-
![\Pr[|X| \geq k\sigma]\leq 2e^{-k^2/4n}](../I/m/4eb8ce9e9e5e91b024dcbf0265dc2d4e.png) for
for 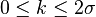
Hoeffding's inequality
Hoeffding's inequality can be stated as follows:
If :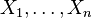 are independent. Assume that the
are independent. Assume that the  are almost surely bounded; that is, assume for
are almost surely bounded; that is, assume for 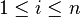 that
that
Then, for the empirical mean of these variables
we have the inequalities (Hoeffding 1963, Theorem 2 [2]):
Bennett's inequality
Bennett's inequality was proved by George Bennett of the University of New South Wales in 1962.[3]
Let X1, … Xn be independent random variables, and assume (for simplicity but without loss of generality) they all have zero expected value. Further assume |Xi| ≤ a almost surely for all i, and let
Then for any t ≥ 0,
where h(u) = (1 + u)log(1 + u) – u,[4] see also Fan et al. (2012) [5] for martingale version of Bennett's inequality and its improvement.
Bernstein's inequality
Bernstein inequalities give bounds on the probability that the sum of random variables deviates from its mean. In the simplest case, let X1, ..., Xn be independent Bernoulli random variables taking values +1 and −1 with probability 1/2, then for every positive  ,
,
Efron–Stein inequality
The Efron–Stein inequality (or influence inequality, or MG bound on variance) bounds the variance of a general function.
Suppose that 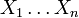 ,
, 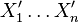 are independent with
are independent with 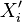 and
and  having the same distribution for all
having the same distribution for all  .
.
Let 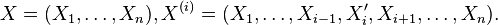 Then
Then
References
- ↑ Chung, Fan. "Old and New Concentration Inequalities". Old and New Concentration Inequalities. Retrieved 2010.
- ↑ Wassily Hoeffding, Probability inequalities for sums of bounded random variables, Journal of the American Statistical Association 58 (301): 13–30, March 1963. (JSTOR)
- ↑ Bennett, G. (1962). "Probability Inequalities for the Sum of Independent Random Variables". Journal of the American Statistical Association 57 (297): 33–45. doi:10.2307/2282438. JSTOR 2282438.
- ↑ Devroye, Luc; Lugosi, Gábor (2001). Combinatorial methods in density estimation. Springer. p. 11. ISBN 978-0-387-95117-1.
- ↑ Fan, X.; Grama, I.; Liu, Q. (2012). "Hoeffding's inequality for supermartingales". Stochastic Processes and their Applications 122: 3545–3559. doi:10.1016/j.spa.2012.06.009.
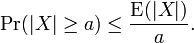
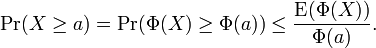
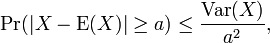
![\operatorname{Var}(X) = \operatorname{E}[(X - \operatorname{E}(X) )^2].](../I/m/04ac25cbef0ec57e3da81d22eb02980b.png)
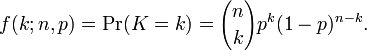
![\lim_{n\to\infty} \Pr[ a\sigma <S_n- np < b\sigma] = \int_a^b \frac{1}{\sqrt{2\pi}}e^{-x^2/2} dx](../I/m/aaaaa9af568387cc6d5e6e14b2f487e6.png)
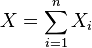
![\Pr[X \leq E(X)-\lambda]\leq e^{-\frac{\lambda^2}{2(Var(X)+\sum_{i=1}^n a_i^2+M\lambda/3)}}](../I/m/f3938507d6c751834f053bfa4ef7b552.png)
![\Pr[X \geq E(X)+\lambda]\leq e^{-\frac{\lambda^2}{2(Var(X)+\sum_{i=1}^n a_i^2+M\lambda/3)}}](../I/m/9ea6262613d510522835fd815844a494.png)
![\Pr(X_i \in [a_i, b_i]) = 1. \!](../I/m/80d027c63f1f91c6c0e4f3bc23011590.png)
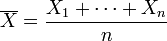
![\Pr(\overline{X} - \mathrm{E}[\overline{X}] \geq t) \leq \exp \left( - \frac{2t^2n^2}{\sum_{i=1}^n (b_i - a_i)^2} \right),\!](../I/m/96fa3c5b5b90898b0b3d24f333e27a29.png)
![\Pr(|\overline{X} - \mathrm{E}[\overline{X}]| \geq t) \leq 2\exp \left( - \frac{2t^2n^2}{\sum_{i=1}^n (b_i - a_i)^2} \right),\!](../I/m/52441e51806393891273978c229d0c0a.png)
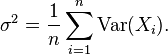
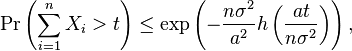
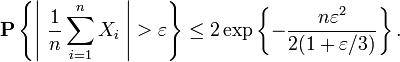
![\mathrm{Var}(f(X)) \leq \frac{1}{2} \sum_{i=1}^{n} E[(f(X)-f(X^{(i)}))^2].](../I/m/7d70ed0ae8966a7c01381c8476d842f1.png)