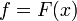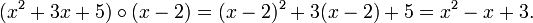Composition ring
In mathematics, a composition ring, introduced in (Adler 1962), is a commutative ring (R, 0, +, −, ·), possibly without an identity 1 (see non-unital ring), together with an operation
such that, for any three elements 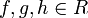 one has
one has
It is not generally the case that 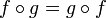 , nor is it generally the case that
, nor is it generally the case that 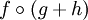 has any algebraic relationship to
has any algebraic relationship to  and
and  .
.
Examples
There are a few ways to make a commutative ring R into a composition ring without introducing anything new.
- Composition may be defined by
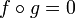 for all f,g. The resulting composition ring is a rather uninteresting.
for all f,g. The resulting composition ring is a rather uninteresting. - Composition may be defined by
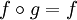 for all f,g. This is the composition rule for constant functions.
for all f,g. This is the composition rule for constant functions. - If R is a boolean ring, then multiplication may double as composition:
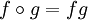 for all f,g.
for all f,g.
More interesting examples can be formed by defining a composition on another ring constructed from R.
- The polynomial ring R[X] can be made into a composition ring with
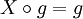 for all g; it follows from the axioms for composition that in general
for all g; it follows from the axioms for composition that in general  will be the result of substituting g for X into f.
will be the result of substituting g for X into f. - The formal power series ring R[[X]] also has a substitution operation, but it is only defined if the series g being substituted has zero constant term (if not, the constant term of the result would be given by an infinite series with arbitrary coefficients). Therefore the subset of R[[X]] formed by power series with zero constant coefficient can be made into a composition ring with composition given by the same substitution rule as for polynomials. Since nonzero constant series are absent, this composition ring does not have a multiplicative unit.
- If R is an integral domain, the field R(X) of rational functions also has a substitution operation derived from that of polynomials: substituting a fraction g1/g2 for X into a polynomial of degree n gives a rational function with denominator
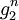 , and substituting into a fraction is given by
, and substituting into a fraction is given by
- However, as for formal power series, the composition cannot always be defined when the right operand g is a constant: in the formula given the denominator
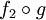 should not be identically zero. One must therefore restrict to a subring of R(X) to have a well-defined composition operation; a suitable subring is given by the rational functions of which the numerator has zero constant term, but the denominator has nonzero constant term. Again this composition ring has no multiplicative unit; if R is a field, it is in fact a subring of the formal power series example.
should not be identically zero. One must therefore restrict to a subring of R(X) to have a well-defined composition operation; a suitable subring is given by the rational functions of which the numerator has zero constant term, but the denominator has nonzero constant term. Again this composition ring has no multiplicative unit; if R is a field, it is in fact a subring of the formal power series example.
- The set of all functions from R to R under pointwise addition and multiplication, and with
 given by composition of functions, is a composition ring. There are numerous variations of this idea, such as the ring of continuous, smooth, holomorphic, or polynomial functions from a ring to itself, when these concepts makes sense.
given by composition of functions, is a composition ring. There are numerous variations of this idea, such as the ring of continuous, smooth, holomorphic, or polynomial functions from a ring to itself, when these concepts makes sense.
For a concrete example take the ring ![{\mathbb Z}[x]](../I/m/3182ba9f80992f4f3bf853027b5dc2a3.png) , considered as the ring of polynomial maps from the integers to itself. A ring endomorphism
, considered as the ring of polynomial maps from the integers to itself. A ring endomorphism
of ![{\mathbb Z}[x]](../I/m/3182ba9f80992f4f3bf853027b5dc2a3.png) is determined by the image under
is determined by the image under 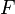 of the variable
of the variable  , which we denote by
, which we denote by
and this image  can be any element of
can be any element of ![{\mathbb Z}[x]](../I/m/3182ba9f80992f4f3bf853027b5dc2a3.png) . Therefore, one may consider the elements
. Therefore, one may consider the elements ![f\in{\mathbb Z}[x]](../I/m/041c300e1899b19ab48add9ab57ea036.png) as endomorphisms and assign
as endomorphisms and assign ![\circ:{\mathbb Z}[x]\times{\mathbb Z}[x]\rightarrow{\mathbb Z}[x]](../I/m/5b762af540c896a3863aa9ff1d266970.png) , accordingly. One easily verifies that
, accordingly. One easily verifies that ![{\mathbb Z}[x]](../I/m/3182ba9f80992f4f3bf853027b5dc2a3.png) satisfies the above axioms. For example, one has
satisfies the above axioms. For example, one has
This example is isomorphic to the given example for R[X] with R equal to 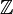 , and also to the subring of all functions
, and also to the subring of all functions 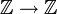 formed by the polynomial functions.
formed by the polynomial functions.
See also
References
- Adler, Irving (1962), "Composition rings", Duke Mathematical Journal 29 (4): 607–623, doi:10.1215/S0012-7094-62-02961-7, ISSN 0012-7094, MR 0142573
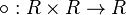
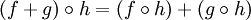
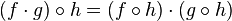
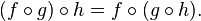
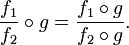
![F:{\mathbb Z}[x]\rightarrow{\mathbb Z}[x]](../I/m/44c1964ca885bd8c2fadfab0083f4ddb.png)