Complex reflection group

In mathematics, a complex reflection group is a group acting on a finite-dimensional complex vector space, that is generated by complex reflections: non-trivial elements that fix a complex hyperplane in space pointwise. (Complex reflections are sometimes called pseudo reflections or unitary reflections or sometimes just reflections.)

Classification

Any real reflection group becomes a complex reflection group if we extend the scalars from R to C. In particular all Coxeter groups or Weyl groups give examples of complex reflection groups.

Any finite complex reflection group is a product of irreducible complex reflection groups, acting on the sum of the corresponding vector spaces. So it is sufficient to classify the irreducible complex reflection groups.

The finite irreducible complex reflection groups were classified by G. C. Shephard and J. A. Todd (1954). They found an infinite family G(m,p,n) depending on 3 positive integer parameters (with p dividing m), and 34 exceptional cases, that they numbered from 4 to 37, listed below. The group G(m,p,n), of order mⁿn!/p, is the semidirect product of the abelian group of order mⁿ/p whose elements are (θ^a₁,θ^a₂, ...,θ^a_n), by the symmetric group S_n acting by permutations of the coordinates, where θ is a primitive mth root of unity and Σa_i≡ 0 mod p; it is an index p subgroup of the generalized symmetric group 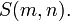$S(m,n).$

Special cases of G(m,p,n):

G(1,1,n) is the Coxeter group A_n−1
G(2,1,n) is the Coxeter group B_n = C_n
G(2,2,n) is the Coxeter group D_n
G(m,p,1) is a cyclic group of order m/p.
G(m,m,2) is the Coxeter group I₂(m) (and the Weyl group G₂ when m = 6).
The group G(m,p,n) acts irreducibly on Cⁿ except in the cases m=1, n>1 (symmetric group) and G(2,2,2) (Klein 4 group), when Cⁿ splits as a sum of irreducible representations of dimensions 1 and n−1.
The only cases when two groups G(m,p,n) are isomorphic as complex reflection groups are that G(ma,pa,1) is isomorphic to G(mb,pb,1) for any positive integers a,b. However there are other cases when two such groups are isomorphic as abstract groups.
The complex reflection group G(2,2,3) is isomorphic as a complex reflection group to G(1,1,4) restricted to a 3-dimensional space.
The complex reflection group G(3,3,2) is isomorphic as a complex reflection group to G(1,1,3) restricted to a 2-dimensional space.
The complex reflection group G(2p,p,1) is isomorphic as a complex reflection group to G(1,1,2) restricted to a 1-dimensional space.

List of irreducible complex reflection groups

There are a few duplicates in the first 3 lines of this list; see the previous section for details.

ST is the Shephard–Todd number of the reflection group.
Rank is the dimension of the complex vector space the group acts on.
Structure describes the structure of the group. The symbol * stands for a central product of two groups. For rank 2, the quotient by the (cyclic) center is the group of rotations of a tetrahedron, octahedron, or icosahedron (T = Alt(4), O = Sym(4), I = Alt(5), of orders 12, 24, 60), as stated in the table. For the notation 2¹⁺⁴, see extra special group.
Order is the number of elements of the group.
Reflections describes the number of reflections: 2⁶4¹² means that there are 6 reflections of order 2 and 12 of order 4.
Degrees gives the degrees of the fundamental invariants of the ring of polynomial invariants. For example, the invariants of group number 4 form a polynomial ring with 2 generators of degrees 4 and 6.

ST	Rank	Structure and names	Order	Reflections	Degrees	Codegrees
1	n−1	Symmetric group G(1,1,n) = Sym(n)	n!	2^{n(n − 1)/2}	2, 3, ...,n	0,1,...,n − 2
2	n	G(m,p,n) m > 1, n > 1, p\|m (G(2,2,2) is reducible)	mⁿn!/p	2^mn(n−1)/2,d^nφ(d) (d\|m/p, d > 1)	m,2m,..,(n − 1)m; mn/p	0,m,..., (n − 1)m if p < m; 0,m,...,(n − 2)m, (n − 1)m − n if p = m
3	1	Cyclic group G(m,1,1) = Z_m	m	d^φ(d) (d\|m, d > 1)	m	0
4	2	Z₂.T = 3[3]3	24	3⁸	4,6	0,2
5	2	Z₆.T = 3[4]3	72	3¹⁶	6,12	0,6
6	2	Z₄.T = 3[6]2	48	2⁶3⁸	4,12	0,8
7	2	Z₁₂.T = 〈3,3,3〉₂	144	2⁶3¹⁶	12,12	0,12
8	2	Z₄.O = 4[3]4	96	2⁶4¹²	8,12	0,4
9	2	Z₈.O = 4[6]2	192	2¹⁸4¹²	8,24	0,16
10	2	Z₁₂.O = 4[4]3	288	2⁶3¹⁶4¹²	12,24	0,12
11	2	Z₂₄.O = 〈4,3,2〉₁₂	576	2¹⁸3¹⁶4¹²	24,24	0,24
12	2	Z₂.O= GL₂(F₃)	48	2¹²	6,8	0,10
13	2	Z₄.O = 〈4,3,2〉₂	96	2¹⁸	8,12	0,16
14	2	Z₆.O = 3[8]2	144	2¹²3¹⁶	6,24	0,18
15	2	Z₁₂.O = 〈4,3,2〉₆	288	2¹⁸3¹⁶	12,24	0,24
16	2	Z₁₀.I = 5[3]5	600	5⁴⁸	20,30	0,10
17	2	Z₂₀.I = 5[6]2	1200	2³⁰5⁴⁸	20,60	0,40
18	2	Z₃₀.I = 5[4]3	1800	3⁴⁰5⁴⁸	30,60	0,30
19	2	Z₆₀.I = 〈5,3,2〉₃₀	3600	2³⁰3⁴⁰5⁴⁸	60,60	0,60
20	2	Z₆.I = 3[5]3	360	3⁴⁰	12,30	0,18
21	2	Z₁₂.I = 3[10]2	720	2³⁰3⁴⁰	12,60	0,48
22	2	Z₄.I = 〈5,3,2〉₂	240	2³⁰	12,20	0,28
23	3	W(H₃) = Z₂ × PSL₂(5), Coxeter	120	2¹⁵	2,6,10	0,4,8
24	3	W(J₃(4)) = Z₂ × PSL₂(7), Klein	336	2²¹	4,6,14	0,8,10
25	3	W(L₃) = W(P₃) = 3¹⁺².SL₂(3), Hessian	648	3²⁴	6,9,12	0,3,6
26	3	W(M₃) =Z₂ ×3¹⁺².SL₂(3), Hessian	1296	2⁹ 3²⁴	6,12,18	0,6,12
27	3	W(J₃(5)) = Z₂ ×(Z₃.Alt(6)), Valentiner	2160	2⁴⁵	6,12,30	0,18,24
28	4	W(F₄) = (SL₂(3)* SL₂(3)).(Z₂ × Z₂) Weyl	1152	2¹²⁺¹²	2,6,8,12	0,4,6,10
29	4	W(N₄) = (Z₄*2^{1 + 4}).Sym(5)	7680	2⁴⁰	4,8,12,20	0,8,12,16
30	4	W(H₄) = (SL₂(5)*SL₂(5)).Z₂ Coxeter	14400	2⁶⁰	2,12,20,30	0,10,18,28
31	4	W(EN₄) = W(O₄) = (Z₄*2^{1 + 4}).Sp₄(2)	46080	2⁶⁰	8,12,20,24	0,12,16,28
32	4	W(L₄) = Z₃ × Sp₄(3)	155520	3⁸⁰	12,18,24,30	0,6,12,18
33	5	W(K₅) = Z₂ ×Ω₅(3) = Z₂ × PSp₄(3) = Z₂ × PSU₄(2)	51840	2⁴⁵	4,6,10,12,18	0,6,8,12,14
34	6	W(K₆)= Z₃.Ω− 6(3).Z₂, Mitchell's group	39191040	2¹²⁶	6,12,18,24,30,42	0,12,18,24,30,36
35	6	W(E₆) = SO₅(3) = O− 6(2) = PSp₄(3).Z₂ = PSU₄(2).Z₂, Weyl	51840	2³⁶	2,5,6,8,9,12	0,3,4,6,7,10
36	7	W(E₇) = Z₂ ×Sp₆(2), Weyl	2903040	2⁶³	2,6,8,10,12,14,18	0,4,6,8,10,12,16
37	8	W(E₈)= Z₂.O+ 8(2), Weyl	696729600	2¹²⁰	2,8,12,14,18,20,24,30	0,6,10,12,16,18,22,28

For more information, including diagrams, presentations, and codegrees of complex reflection groups, see the tables in (Michel Broué, Gunter Malle & Raphaël Rouquier 1998).

Degrees

Shephard and Todd proved that a finite group acting on a complex vector space is a complex reflection group if and only if its ring of invariants is a polynomial ring (Chevalley–Shephard–Todd theorem). For 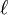$\ell$ being the rank of the reflection group, the degrees 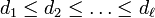$d_1 \leq d_2 \leq \ldots \leq d_\ell$ of the generators of the ring of invariants are called degrees of W and are listed in the column above headed "degrees". They also showed that many other invariants of the group are determined by the degrees as follows:

The center of an irreducible reflection group is cyclic of order equal to the greatest common divisor of the degrees.

The order of a complex reflection group is the product of its degrees.

The number of reflections is the sum of the degrees minus the rank.

An irreducible complex reflection group comes from a real reflection group if and only if it has an invariant of degree 2.

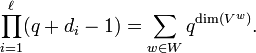
The degrees d_i satisfy the formula $\prod_{i=1}^\ell(q+d_i-1)= \sum_{w\in W}q^{\dim(V^w)}.$

Codegrees

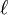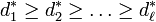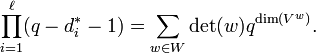
For $\ell$ being the rank of the reflection group, the codegrees $d^*_1 \geq d^*_2 \geq \ldots \geq d^*_\ell$ of W can be defined by $\prod_{i=1}^\ell(q-d^*_i-1)= \sum_{w\in W}\det(w)q^{\dim(V^w)}.$

For a real reflection group, the codegrees are the degrees minus 2.

The number of reflection hyperplanes is the sum of the codegrees plus the rank.

Well-generated complex reflection groups

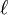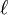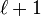An irreducible complex reflection group of rank $\ell$ is generated by $\ell$ or by $\ell+1$ reflections. It is said to be well-generated if it is generated by 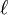$\ell$ reflections ; it is proved that this is equivalent to the property 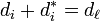$d_i + d^*_i = d_\ell$ for all 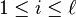$1 \leq i \leq \ell$ . For irreducible well-generated complex reflection groups, the Coxeter number 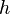$h$ is defined to be the largest degree, 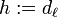$h := d_\ell$ . A reducible complex reflection group is said to be well-generated if it is a product of irreducible well-generated complex reflection groups. Any finite real reflection group is well-generated.

References

Broué, Michel; Malle, Gunter; Rouquier, Raphaël (1995), "On complex reflection groups and their associated braid groups", Representations of groups (Banff, AB, 1994), CMS Conf. Proc. 16, Providence, R.I.: American Mathematical Society, pp. 1–13, MR 1357192
Broué, Michel; Malle, Gunter; Rouquier, Raphaël (1998), "Complex reflection groups, braid groups, Hecke algebras", Journal für die reine und angewandte Mathematik 500: 127–190, doi:10.1515/crll.1998.064, ISSN 0075-4102, MR 1637497, CiteSeerX: 10.1.1.128.2907
Deligne, Pierre (1972), "Les immeubles des groupes de tresses généralisés", Inventiones Mathematicae 17 (4): 273–302, doi:10.1007/BF01406236, ISSN 0020-9910, MR 0422673
Hiller, Howard Geometry of Coxeter groups. Research Notes in Mathematics, 54. Pitman (Advanced Publishing Program), Boston, Mass.-London, 1982. iv+213 pp. ISBN 0-273-08517-4*
Lehrer, Gustav I.; Taylor, Donald E. (2009), Unitary reflection groups, Australian Mathematical Society Lecture Series 20, Cambridge University Press, ISBN 978-0-521-74989-3, MR 2542964
Shephard, G. C.; Todd, J. A. (1954), "Finite unitary reflection groups", Canadian Journal of Mathematics. Journal Canadien de Mathématiques (Canadian Mathematical Society) 6: 274–304, doi:10.4153/CJM-1954-028-3, ISSN 0008-414X, MR 0059914

External links

MAGMA Computational Algebra System page