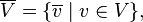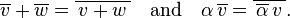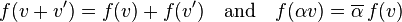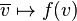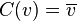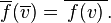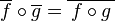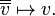Complex conjugate vector space
In mathematics, the (formal) complex conjugate of a complex vector space 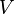 is the complex vector space
is the complex vector space 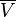 consisting of all formal complex conjugates of elements of
consisting of all formal complex conjugates of elements of 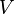 . That is,
. That is, 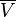 is a vector space whose elements are in one-to-one correspondence with the elements of
is a vector space whose elements are in one-to-one correspondence with the elements of 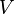 :
:
with the following rules for addition and scalar multiplication:
Here 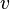 and
and 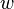 are vectors in
are vectors in 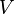 ,
,  is a complex number, and
is a complex number, and 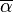 denotes the complex conjugate of
denotes the complex conjugate of  .
.
More concretely, the complex conjugate vector space is the same underlying real vector space (same set of points, same vector addition and real scalar multiplication) with the conjugate linear complex structure J (different multiplication by i).
Antilinear maps
If 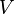 and
and 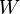 are complex vector spaces, a function
are complex vector spaces, a function 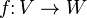 is antilinear if
is antilinear if
for all 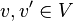 and
and 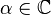 .
.
One reason to consider the vector space 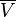 is that it makes antilinear maps into linear maps. Specifically, if
is that it makes antilinear maps into linear maps. Specifically, if 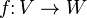 is an antilinear map, then the corresponding map
is an antilinear map, then the corresponding map 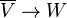 defined by
defined by
is linear. Conversely, any linear map defined on 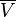 gives rise to an antilinear map on
gives rise to an antilinear map on 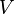 .
.
One way of thinking about this correspondence is that the map 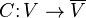 defined by
defined by
is an antilinear bijection. Thus if 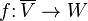 is linear, then composition
is linear, then composition 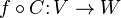 is antilinear, and vice versa.
is antilinear, and vice versa.
Conjugate linear maps
Any linear map 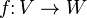 induces a conjugate linear map
induces a conjugate linear map 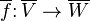 , defined by the formula
, defined by the formula
The conjugate linear map 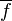 is linear. Moreover, the identity map on
is linear. Moreover, the identity map on 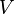 induces the identity map
induces the identity map 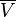 , and
, and
for any two linear maps 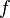 and
and 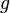 . Therefore, the rules
. Therefore, the rules 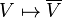 and
and 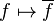 define a functor from the category of complex vector spaces to itself.
define a functor from the category of complex vector spaces to itself.
If 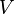 and
and 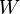 are finite-dimensional and the map
are finite-dimensional and the map 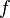 is described by the complex matrix
is described by the complex matrix 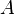 with respect to the bases
with respect to the bases 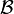 of
of 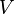 and
and 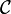 of
of 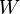 , then the map
, then the map 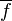 is described by the complex conjugate of
is described by the complex conjugate of 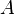 with respect to the bases
with respect to the bases 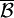 of
of 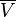 and
and 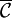 of
of 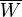 .
.
Structure of the conjugate
The vector spaces 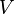 and
and 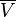 have the same dimension over the complex numbers and are therefore isomorphic as complex vector spaces. However, there is no natural isomorphism from
have the same dimension over the complex numbers and are therefore isomorphic as complex vector spaces. However, there is no natural isomorphism from 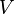 to
to 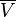 . (The map
. (The map 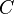 is not an isomorphism, since it is antilinear.)
is not an isomorphism, since it is antilinear.)
The double conjugate 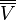 is naturally isomorphic to
is naturally isomorphic to 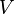 , with the isomorphism
, with the isomorphism 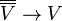 defined by
defined by
Usually the double conjugate of 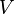 is simply identified with
is simply identified with 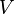 .
.
Complex conjugate of a Hilbert space
Given a Hilbert space  (either finite or infinite dimensional), its complex conjugate
(either finite or infinite dimensional), its complex conjugate 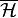 is the same vector space as its continuous dual space
is the same vector space as its continuous dual space 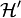 .
There is one-to-one antilinear correspondence between continuous linear functionals and vectors.
In other words, any continuous linear functional on
.
There is one-to-one antilinear correspondence between continuous linear functionals and vectors.
In other words, any continuous linear functional on  is an inner multiplication to some fixed vector, and vice versa.
is an inner multiplication to some fixed vector, and vice versa.
Thus, the complex conjugate to a vector  , particularly in finite dimension case, may be denoted as
, particularly in finite dimension case, may be denoted as 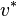 (v-star, a row vector which is the conjugate transpose to a column vector
(v-star, a row vector which is the conjugate transpose to a column vector  ).
In quantum mechanics, the conjugate to a ket vector
).
In quantum mechanics, the conjugate to a ket vector 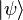 is denoted as
is denoted as 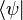 – a bra vector (see bra–ket notation).
– a bra vector (see bra–ket notation).
See also
References
- Budinich, P. and Trautman, A. The Spinorial Chessboard. Spinger-Verlag, 1988. ISBN 0-387-19078-3. (complex conjugate vector spaces are discussed in section 3.3, pag. 26).