Complex Lie group

In geometry, a complex Lie group is a complex-analytic manifold that is also a group in such a way 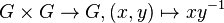$G \times G \to G, (x, y) \mapsto x y^{-1}$ is holomorphic. Basic examples are 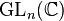$\operatorname{GL}_n(\mathbb{C})$ , the general linear groups over the complex numbers. A connected compact complex Lie group is precisely a complex torus (not to be confused with the complex Lie group $\mathbb C^*$ ). Any finite group may be given the structure of a complex Lie group. A complex semisimple Lie group is an algebraic group.

Examples

See also: Table of Lie groups

A finite-dimensional vector space over the complex numbers (in particular, complex Lie algebra) is a complex Lie group in an obvious way.
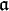A connected compact complex Lie group A of dimension g is of the form $\mathbb{C}^g/L$ where L is a discrete subgroup. Indeed, its Lie algebra $\mathfrak{a}$ can be shown to be abelian and then 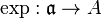$\operatorname{exp}: \mathfrak{a} \to A$ is a surjective morphism of complex Lie groups, showing A is of the form described.
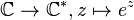$\mathbb{C} \to \mathbb{C}^*, z \mapsto e^z$ is an example of a morphism of complex Lie groups that does not come from a morphism of algebraic groups. Since 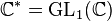$\mathbb{C}^* = \operatorname{GL}_1(\mathbb{C})$ , this is also an example of a representation of a complex Lie group that is not algebraic.
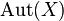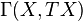Let X be a compact complex manifold. Then, as in the real case, $\operatorname{Aut}(X)$ is a complex Lie group whose Lie algebra is $\Gamma(X, TX)$ .
Let K be a connected compact Lie group. Then there exists a unique connected complex Lie group G such that (i) 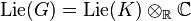$\operatorname{Lie} (G) = \operatorname{Lie} (K) \otimes_{\mathbb{R}} \mathbb{C}$ (ii) K is a maximal compact subgroup of G. It is called the complexification of K. For example, 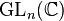$\operatorname{GL}_n(\mathbb{C})$ is the complexification of the unitary group. If K is acting on a compact kähler manifold X, then the action of K extends to that of G.

References

Lee, Dong Hoon (2002), The Structure of Complex Lie Groups, Boca Raton, FL: Chapman & Hall/CRC, ISBN 1-58488-261-1, MR 1887930
Serre, Jean-Pierre (1993), Gèbres