Complex-oriented cohomology theory
In algebraic topology, a complex-orientable cohomology theory is a multiplicative cohomology theory E such that the restriction map 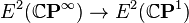 is surjective. An element of
is surjective. An element of 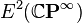 that restricts to the canonical generator of the reduced theory
that restricts to the canonical generator of the reduced theory 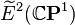 is called a complex orientation. The notion is central to Quillen's work relating cohomology to formal group laws.
is called a complex orientation. The notion is central to Quillen's work relating cohomology to formal group laws.
If 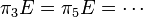 , then E is complex-orientable.
, then E is complex-orientable.
Examples:
- An ordinary cohomology with any coefficient ring R is complex orientable, as
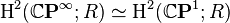 .
. - A complex K-theory, denoted by K, is complex-orientable, as
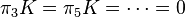 (Bott periodicity theorem)
(Bott periodicity theorem) - Complex cobordism, whose spectrum is denoted by MU, is complex-orientable.
A complex orientation, call it t, gives rise to a formal group law as follows: let m be the multiplication
where ![[x]](../I/m/3e5314e9fd31509fdeb83faa0f729ba2.png) denotes a line passing through x in the underlying vector space
denotes a line passing through x in the underlying vector space ![\mathbb{C}[t]](../I/m/892dc911207503fcf853b65f081afa60.png) of
of 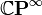 . Viewing
. Viewing
![E^*(\mathbb{C}\mathbf{P}^\infty) = \varprojlim E^*(\mathbb{C}\mathbf{P}^n) = \varprojlim R[t]/(t^{n+1}) = R[\![t]\!], \quad R =\pi_* E = \oplus \pi_{2n} E](../I/m/a8d8f08136ed5948cd339aa0237f1ccf.png) ,
,
let 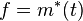 be the pullback of t along m. It lives in
be the pullback of t along m. It lives in
and one can show it is a formal group law (e.g., satisfies associativity).
![\mathbb{C}\mathbf{P}^\infty \times \mathbb{C}\mathbf{P}^\infty \to \mathbb{C}\mathbf{P}^\infty, ([x], [y]) \mapsto [xy]](../I/m/a61ea99957ca3965665529d71cdfe5b3.png)
![E^*(\mathbb{C}\mathbf{P}^\infty \times \mathbb{C}\mathbf{P}^\infty) = \varprojlim E^*(\mathbb{C}\mathbf{P}^n \times \mathbb{C}\mathbf{P}^m) = \varprojlim R[x,y]/(x^{n+1},y^{m+1}) = R[\![x, y]\!]](../I/m/ea941227029419db43f2905c1aa82c3d.png)