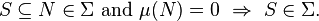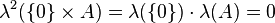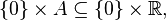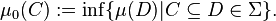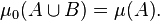Complete measure

In mathematics, a complete measure (or, more precisely, a complete measure space) is a measure space in which every subset of every null set is measurable (having measure zero). More formally, (X, Σ, μ) is complete if and only if

S \subseteq N \in \Sigma \mbox{ and } \mu(N) = 0\ \Rightarrow\ S \in \Sigma.

Motivation

The need to consider questions of completeness can be illustrated by considering the problem of product spaces.

Suppose that we have already constructed Lebesgue measure on the real line: denote this measure space by (R, B, λ). We now wish to construct some two-dimensional Lebesgue measure λ² on the plane R² as a product measure. Naïvely, we would take the σ-algebra on R² to be B ⊗ B, the smallest σ-algebra containing all measurable "rectangles" A₁ × A₂ for A_i ∈ B.

While this approach does define a measure space, it has a flaw. Since every singleton set has one-dimensional Lebesgue measure zero,

\lambda^{2} ( \{ 0 \} \times A ) = \lambda ( \{ 0 \} ) \cdot \lambda (A) = 0

for "any" subset A of R. However, suppose that A is a non-measurable subset of the real line, such as the Vitali set. Then the λ²-measure of {0} × A is not defined, but

\{ 0 \} \times A \subseteq \{ 0 \} \times \mathbb{R},

and this larger set does have λ²-measure zero. So, this "two-dimensional Lebesgue measure" as just defined is not complete, and some kind of completion procedure is required.

Construction of a complete measure

Given a (possibly incomplete) measure space (X, Σ, μ), there is an extension (X, Σ₀, μ₀) of this measure space that is complete. The smallest such extension (i.e. the smallest σ-algebra Σ₀) is called the completion of the measure space.

The completion can be constructed as follows:

let Z be the set of all subsets of μ-measure zero subsets of X (intuitively, those elements of Z that are not already in Σ are the ones preventing completeness from holding true);
let Σ₀ be the σ-algebra generated by Σ and Z (i.e. the smallest σ-algebra that contains every element of Σ and of Z);
there is a unique extension μ₀ of μ to Σ₀ given by the infimum

\mu_{0} (C) := \inf \{ \mu (D) | C \subseteq D \in \Sigma \}.

Then (X, Σ₀, μ₀) is a complete measure space, and is the completion of (X, Σ, μ).

In the above construction it can be shown that every member of Σ₀ is of the form A ∪ B for some A ∈ Σ and some B ∈ Z, and

\mu_{0} (A \cup B) = \mu (A).

Examples

Borel measure as defined on the Borel σ-algebra generated by the open intervals of the real line is not complete, and so the above completion procedure must be used to define the complete Lebesgue measure. This is illustrated by the fact that the set of all Borel sets over the reals has the same cardinality as the reals. While the Cantor Set is a Borel set, has measure zero, and its power set has cardinality strictly greater than that of the reals. Thus there is a subset of the Cantor set that is not contained in the Borel sets. Hence, the Borel measure is not complete.
n-dimensional Lebesgue measure is the completion of the n-fold product of the one-dimensional Lebesgue space with itself. It is also the completion of the Borel measure, as in the one-dimensional case.

Properties

Maharam's theorem states that every complete measure space is decomposable into a measure on the continuum, and a finite or countable counting measure.

References

Terekhin, A.P. (2001), "Complete measure", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4