Comparison of optimization software
Given a system transforming a set of inputs to output values, described by a mathematical function f, optimization refers to the generation and selection of a best solution from some set of available alternatives,[1] by systematically choosing input values from within an allowed set, computing the value of the function, and recording the best value found during the process. Many real-world and theoretical problems may be modeled in this general framework. For example, the inputs can be design parameters of a motor, the output can be the power consumption, or the inputs can be business choices and the output can be the obtained profit, or the inputs can describe the configuration of a physical system and the output can be its energy.
An optimization problem can be represented in the following way
- Given: a function f : A
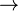R from some set A to the real numbers - Search for: an element x0 in A such that f(x0) ≤ f(x) for all x in A ("minimization").
Typically, A is some subset of the Euclidean space Rn, often specified by a set of constraints, equalities or inequalities that the members of A have to satisfy. Maximization can be reduced to minimization by multiplying the function by minus one.
The use of optimization software requires that the function f is defined in a suitable programming language and linked to the optimization software. The optimization software will deliver input values in A, the software module realizing f will deliver the computed value f(x). In this manner, a clear separation of concerns is obtained: different optimization software modules can be easily tested on the same function f, or a given optimization software can be used for different functions f.
The following tables provide a comparison of optimization software libraries, either specialized or general purpose libraries with significant optimization coverage.
| Language | Latest stable version | Academic/noncommercial use is free |
Can be used in proprietary aps |
License | Notes | |
|---|---|---|---|---|---|---|
| ALGLIB | C++, C#, FreePascal, VBA | 3.8.0 / August 2013 | Yes | Yes | Dual (Commercial, GPL) | General purpose library, includes optimization package. |
| AMPL | C | October 2013 | Yes | Yes | Dual (Commercial, academic) | A popular algebraic modeling language for linear, mixed-integer and nonlinear optimization. Student and AMPL for courses versions are available for free. |
| GNU Scientific Library | C | 1.16 / July 2013 | Yes | No | GPL | Free library provided by GNU project. |
| GNU Linear Programming Kit | C | 4.52 / July 2013 | Yes | No | GPL | Free library for linear programming (LP) and mixed integer programming (MIP). |
| IMSL Numerical Libraries | C, Java, C#, Fortran, Python | many components | No | Yes | Proprietary | |
| LIONsolver | C++, Java | 2.0.198 / October 2011 | Yes | Yes | Proprietary | Support for interactive and learning optimization,
according to RSO principles .[2] |
| MKL | C++, Fortran | 11.1 / October 2013 | No | Yes | Proprietary | Numerical library from Intel. MKL is specialized on linear algebra, but contains some optimization-related functionality. |
| NAG Numerical Libraries | C, Fortran | Mark 24 / October 2013 | No | Yes | Proprietary | |
| NMath | C# | 5.3 / May 2013 | No | Yes | Proprietary | C# numerical library built on top of MKL. |
| OptaPlanner | Java | 6.0.1.Final / Dec 2013 | Yes | Yes | ASL | Lightweight optimization solver in Java |
| SciPy | Python | 0.13.1 / November 2013 | Yes | Yes | BSD | General purpose numerical library from Enthought. |
References
- ↑ "The Nature of Mathematical Programming," Mathematical Programming Glossary, INFORMS Computing Society.
- ↑ Battiti, Roberto; Mauro Brunato; Franco Mascia (2008). Reactive Search and Intelligent Optimization. Springer Verlag. ISBN 978-0-387-09623-0.
External links
- OR/MS Today: 2013 Linear Programming Software Survey
- OR/MS Today: 1998 Nonlinear Programming Software Survey
| ||||||||||||||||||||||||||||||||||||||||||||||||||