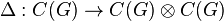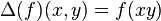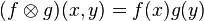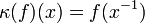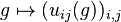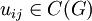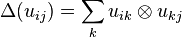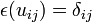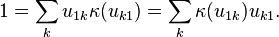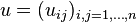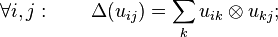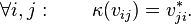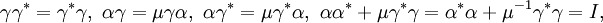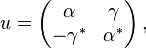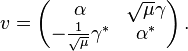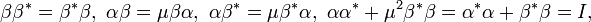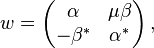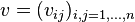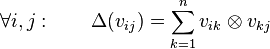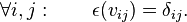Compact quantum group
In mathematics, a compact quantum group is an abstract structure on a unital separable C*-algebra axiomatized from those that exist on the commutative C*-algebra of "continuous complex-valued functions" on a compact quantum group.
The basic motivation for this theory comes from the following analogy. The space of complex-valued functions on a compact Hausdorff topological space forms a commutative C*-algebra. On the other hand, by the Gelfand Theorem, a commutative C*-algebra is isomorphic to the C*-algebra of continuous complex-valued functions on a compact Hausdorff topological space, and the topological space is uniquely determined by the C*-algebra up to homeomorphism.
S. L. Woronowicz [1] introduced the important concept of compact matrix quantum groups, which he initially called compact pseudogroups. Compact matrix quantum groups are abstract structures on which the "continuous functions" on the structure are given by elements of a C*-algebra. The geometry of a compact matrix quantum group is a special case of a noncommutative geometry.
Formulation
For a compact topological group, G, there exists a C*-algebra homomorphism
where C(G) ⊗ C(G) is the minimal C*-algebra tensor product — the completion of the algebraic tensor product of C(G) and C(G)) — such that
for all 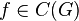 , and for all
, and for all 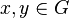 , where
, where
for all 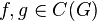 and all
and all 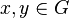 . There also exists a linear multiplicative mapping
. There also exists a linear multiplicative mapping
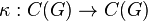 ,
,
such that
for all 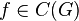 and all
and all 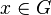 . Strictly speaking, this does not make C(G) into a Hopf algebra, unless G is finite.
. Strictly speaking, this does not make C(G) into a Hopf algebra, unless G is finite.
On the other hand, a finite-dimensional representation of G can be used to generate a *-subalgebra of C(G) which is also a Hopf *-algebra. Specifically, if
is an n-dimensional representation of G, then
for all i, j, and
for all i, j. It follows that the *-algebra generated by 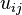 for all i, j and
for all i, j and 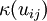 for all i, j is a Hopf *-algebra: the counit is determined by
for all i, j is a Hopf *-algebra: the counit is determined by
for all 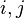 (where
(where 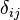 is the Kronecker delta), the antipode is κ, and the unit is given by
is the Kronecker delta), the antipode is κ, and the unit is given by
Compact Matrix Quantum Groups
As a generalization, a compact matrix quantum group is defined as a pair (C, u), where C is a C*-algebra and
is a matrix with entries in C such that
- The *-subalgebra, C0, of C, which is generated by the matrix elements of u, is dense in C;
- There exists a C*-algebra homomorphism, called the comultiplication, Δ : C → C ⊗ C (here C ⊗ C is the C*-algebra tensor product - the completion of the algebraic tensor product of C and C) such that
- There exists a linear antimultiplicative map, called the coinverse, κ : C0 → C0 such that
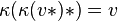 for all
for all 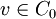 and
and 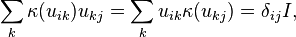 where I is the identity element of C. Since κ is antimultiplicative, κ(vw) = κ(w)κ(v) for all
where I is the identity element of C. Since κ is antimultiplicative, κ(vw) = κ(w)κ(v) for all 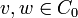 .
.
As a consequence of continuity, the comultiplication on C is coassociative.
In general, C is a bialgebra, and C0 is a Hopf *-algebra.
Informally, C can be regarded as the *-algebra of continuous complex-valued functions over the compact matrix quantum group, and u can be regarded as a finite-dimensional representation of the compact matrix quantum group.
Compact Quantum Groups
For C*-algebras A and B acting on the Hilbert spaces H and K respectively, their minimal tensor product is defined to be the norm completion of the algebraic tensor product A ⊗ B in B(H ⊗ K); the norm completion is also denoted by A ⊗ B.
A compact quantum group[2][3] is defined as a pair (C, Δ), where C is a unital separable C*-algebra and
- Δ : C → C ⊗ C is a C*-algebra unital homomorphism satisfying (Δ ⊗ id) Δ = (id ⊗ Δ) Δ;
- the sets {(C ⊗ 1) Δ(C)} and {(1 ⊗ C) Δ(C)} are dense in C ⊗ C.
Representations
A representation of the compact matrix quantum group is given by a corepresentation of the Hopf *-algebra[4] Furthermore, a representation, v, is called unitary if the matrix for v is unitary, or equivalently, if
Example
An example of a compact matrix quantum group is SUμ(2),[5] where the parameter μ is a positive real number.
First Definition
SUμ(2) = (C(SUμ(2)), u), where C(SUμ(2)) is the C*-algebra generated by α and γ, subject to
and
so that the comultiplication is determined by 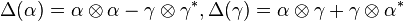 , and the coinverse is determined by
, and the coinverse is determined by 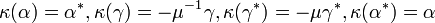 . Note that u is a representation, but not a unitary representation. u is equivalent to the unitary representation
. Note that u is a representation, but not a unitary representation. u is equivalent to the unitary representation
Second Definition
SUμ(2) = (C(SUμ(2)), w), where C(SUμ(2)) is the C*-algebra generated by α and β, subject to
and
so that the comultiplication is determined by 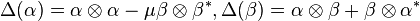 , and the coinverse is determined by
, and the coinverse is determined by 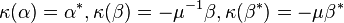 ,
, 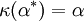 . Note that w is a unitary representation. The realizations can be identified by equating
. Note that w is a unitary representation. The realizations can be identified by equating 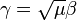 .
.
Limit Case
If μ = 1, then SUμ(2) is equal to the concrete compact group SU(2).
References
- ↑ Woronowicz, S.L. "Compact Matrix Pseudogrooups", Commun. Math. Phys. 111 (1987), 613-665
- ↑ Woronowicz, S.L. "Compact Quantum Groups". Notes from http://www.fuw.edu.pl/~slworono/PDF-y/CQG3.pdf
- ↑ van Daele, A. and Maes, Ann. "Notes on compact quantum groups", arXiv:math/9803122
- ↑ a corepresentation of a counital coassiative coalgebra A is a square matrix
- ↑ van Daele, A. and Wang, S. "Universal quantum groups" Int. J. of Math. (1996), 255-263.