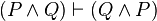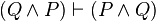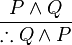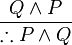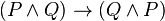Commutativity of conjunction

In propositional logic, the commutativity of conjunction is a valid argument form and truth-functional tautology. It is considered to be a law of classical logic. It is the principle that the conjuncts of a logical conjunction may switch places with each other, while preserving the truth-value of the resulting proposition.[1]

Formal notation

Commutativity of conjunction can be expressed in sequent notation as:

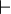(P \and Q) \vdash (Q \and P)

and

(Q \and P) \vdash (P \and Q)

where \vdash is a metalogical symbol meaning that 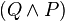(Q \and P) is a syntactic consequence of 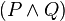(P \and Q), in the one case, and 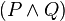(P \and Q) is a syntactic consequence of 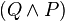(Q \and P) in the other, in some logical system;

or in rule form:

\frac{P \and Q}{\therefore Q \and P}

and

\frac{Q \and P}{\therefore P \and Q}

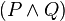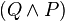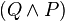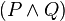where the rule is that wherever an instance of "(P \and Q)" appears on a line of a proof, it can be replaced with "(Q \and P)" and wherever an instance of "(Q \and P)" appears on a line of a proof, it can be replaced with "(P \and Q)";

or as the statement of a truth-functional tautology or theorem of propositional logic:

(P \and Q) \to (Q \and P)

and

(Q \and P) \to (P \and Q)

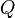where P and Q are propositions expressed in some formal system.

Generalized principle

For any propositions H1, H2, ... Hn, and permutation σ(n) of the numbers 1 through n, it is the case that:

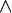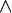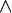H1 \land H2 \land ... \land Hn

is equivalent to

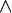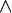Hσ(1) \land Hσ(2) \land Hσ(n).

For example, if H1 is

It is raining

H2 is

Socrates is mortal

and H3 is

2+2=4

then

It is raining and Socrates is mortal and 2+2=4

is equivalent to

Socrates is mortal and 2+2=4 and it is raining

and the other orderings of the predicates.

References

  1. ↑ Elliott Mendelson (1997). Introduction to Mathematical Logic. CRC Press. ISBN 0-412-80830-7.