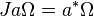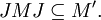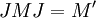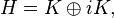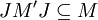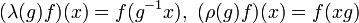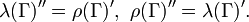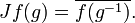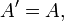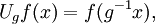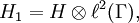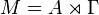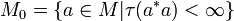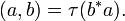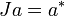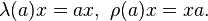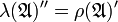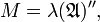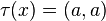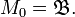Commutation theorem

In mathematics, a commutation theorem explicitly identifies the commutant of a specific von Neumann algebra acting on a Hilbert space in the presence of a trace. The first such result was proved by F.J. Murray and John von Neumann in the 1930s and applies to the von Neumann algebra generated by a discrete group or by the dynamical system associated with a measurable transformation preserving a probability measure. Another important application is in the theory of unitary representations of unimodular locally compact groups, where the theory has been applied to the regular representation and other closely related representations. In particular this framework led to an abstract version of the Plancherel theorem for unimodular locally compact groups due to Irving Segal and Forrest Stinespring and an abstract Plancherel theorem for spherical functions associated with a Gelfand pair due to Roger Godement. Their work was put in final form in the 1950s by Jacques Dixmier as part of the theory of Hilbert algebras. It was not until the late 1960s, prompted partly by results in algebraic quantum field theory and quantum statistical mechanics due to the school of Rudolf Haag, that the more general non-tracial Tomita–Takesaki theory was developed, heralding a new era in the theory of von Neumann algebras.

Commutation theorem for finite traces

Let H be a Hilbert space and M a von Neumann algebra on H with a unit vector Ω such that

M Ω is dense in H
M ' Ω is dense in H, where M ' denotes the commutant of M
(abΩ, Ω) = (baΩ, Ω) for all a, b in M.

The vector Ω is called a cyclic-separating trace vector. It is called a trace vector because the last condition means that the matrix coefficient corresponding to Ω defines a tracial state on M. It is called cyclic since Ω generates H as a topological M-module. It is called separating because if aΩ = 0 for a in M, then aM'Ω= (0), and hence a = 0.

It follows that the map

Ja\Omega=a^*\Omega

for a in M defines a conjugate-linear isometry of H with square the identity J² = I. The operator J is usually called the modular conjugation operator.

It is immediately verified that JMJ and M commute on the subspace M Ω, so that

JMJ\subseteq M^\prime.

The commutation theorem of Murray and von Neumann states that

JMJ=M^\prime

One of the easiest ways to see this^[1] is to introduce K, the closure of the real subspace M_sa Ω, where M_sa denotes the self-adjoint elements in M. It follows that

H=K\oplus iK,

an orthogonal direct sum for the real part of inner product. This is just the real orthogonal decomposition for the ±1 eigenspaces of J. On the other hand for a in M_sa and b in M'_sa, the inner product (abΩ, Ω) is real, because ab is self-adjoint. Hence K is unaltered if M is replaced by M '.

In particular Ω is a trace vector for M' and J is unaltered if M is replaced by M '. So the opposite inclusion

JM^\prime J\subseteq M

follows by reversing the roles of M and M'.

Examples

One of the simplest cases of the commutation theorem, where it can easily be seen directly, is that of a finite group Γ acting on the finite-dimensional inner product space 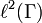$\ell^2(\Gamma)$ by the left and right regular representations λ and ρ. These unitary representations are given by the formulas

(\lambda(g) f)(x)=f(g^{-1}x),\,\,(\rho(g)f)(x)=f(xg)

for f in

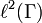\ell^2(\Gamma)

and the commutation theorem implies that

\lambda(\Gamma)^{\prime\prime}=\rho(\Gamma)^\prime, \,\, \rho(\Gamma)^{\prime\prime}=\lambda(\Gamma)^\prime.

The operator J is given by the formula

Jf(g)=\overline{f(g^{-1})}.

Exactly the same results remain true if Γ is allowed to be any countable discrete group.^[2] The von Neumann algebra λ(Γ)' ' is usually called the group von Neumann algebra of Γ.

Another important example is provided by a probability space (X, μ). The Abelian von Neumann algebra A = L^∞(X, μ) acts by multiplication operators on H = L²(X, μ) and the constant function 1 is a cyclic-separating trace vector. It follows that

A^{\prime}=A,

so that A is a maximal Abelian subalgebra of B(H), the von Neumann algebra of all bounded operators on H.

The third class of examples combines the above two. Coming from ergodic theory, it was one of von Neumann's original motivations for studying von Neumann algebras. Let (X, μ) be a probability space and let Γ be a countable discrete group of measure-preserving transformations of (X, μ). The group therefore acts unitarily on the Hilbert space H = L²(X, μ) according to the formula

U_g f(x) = f(g^{-1}x),

for f in H and normalises the Abelian von Neumann algebra A = L^∞(X, μ). Let

H_1=H\otimes \ell^2(\Gamma),

a tensor product of Hilbert spaces.^[3] The group–measure space construction or crossed product von Neumann algebra

M = A \rtimes \Gamma

is defined to be the von Neumann algebra on H₁ generated by the algebra

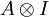A\otimes I

and the normalising operators

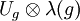U_g\otimes \lambda(g)

.^[4]

The vector

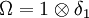\Omega=1\otimes \delta_1

is a cyclic-separating trace vector. Moreover the modular conjugation operator J and commutant M ' can be explicitly identified.

One of the most important cases of the group–measure space construction is when Γ is the group of integers Z, i.e. the case of a single invertible measurable transformation T. Here T must preserve the probability measure μ. Semifinite traces are required to handle the case when T (or more generally Γ) only preserves an infinite equivalent measure; and the full force of the Tomita–Takesaki theory is required when there is no invariant measure in the equivalence class, even though the equivalence class of the measure is preserved by T (or Γ).^[5]^[6]

Commutation theorem for semifinite traces

Let M be a von Neumann algebra and M₊ the set of positive operators in M. By definition,^[2] a semifinite trace (or sometimes just trace) on M is a functional τ from M₊ into [0,∞] such that

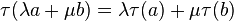$\tau(\lambda a + \mu b) = \lambda \tau(a) + \mu \tau(b)$ for a, b in M₊ and λ, μ ≥ 0 (semilinearity);
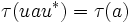$\tau(uau^*)=\tau(a)$ for a in M₊ and u a unitary operator in M (unitary invariance);
τ is completely additive on orthogonal families of projections in M (normality);
each projection in M is as orthogonal direct sum of projections with finite trace (semifiniteness).

If in addition τ is non-zero on every non-zero projection, then τ is called a faithful trace.

If τ is a faithul trace on M, let H = L²(M, τ) be the Hilbert space completion of the inner product space

M_0=\{a\in M| \tau(a^*a) <\infty\}

with respect to the inner product

(a,b)=\tau(b^*a).

The von Neumann algebra M acts by left multiplication on H and can be identified with its image. Let

Ja=a^*

for a in M₀. The operator J is again called the modular conjugation operator and extends to a conjugate-linear isometry of H satisfying J² = I. The commutation theorem of Murray and von Neumann

JMJ=M^\prime

is again valid in this case. This result can be proved directly by a variety of methods,^[2] but follows immediately from the result for finite traces, by repeated use of the following elementary fact:

If M₁

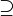\supseteq

M₂ are two von Neumann algebras such that p_n M₁ = p_n M₂ for a family of projections p_n in the commutant of M₁ increasing to I in the strong operator topology, then M₁ = M₂.

Hilbert algebras

Definition

A Hilbert algebra^[2]^[11]^[12] is an algebra 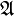$\mathfrak{A}$ with involution x→x* and an inner product (,) such that

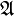(a,b)=(b*,a*) for a, b in $\mathfrak{A}$ ;
left multiplication by a fixed a in 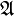$\mathfrak{A}$ is a bounded operator;
* is the adjoint, in other words (xy,z) = (y, x*z);
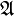the linear span of all products xy is dense in $\mathfrak{A}$ .

Examples

The Hilbert–Schmidt operators on an infinite-dimensional Hilbert space form a Hilbert algebra with inner product (a,b) = Tr (b*a).
If (X, μ) is an infinite measure space, the algebra L^∞ (X) 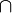$\cap$ L²(X) is a Hilbert algebra with the usual inner product from L²(X).
If M is a von Neumann algebra with faithful semifinite trace τ, then the *-subalgebra M₀ defined above is a Hilbert algebra with inner product (a, b) = τ(b*a).
If G is a unimodular locally compact group, the convolution algebra L¹(G) 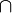$\cap$ L²(G) is a Hilbert algebra with the usual inner product from L²(G).
If (G, K) is a Gelfand pair, the convolution algebra L¹(K\G/K) 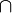$\cap$ L²(K\G/K) is a Hilbert algebra with the usual inner product from L²(G); here L^p(K\G/K) denotes the closed subspace of K-biinvariant functions in L^p(G).
Any dense *-subalgebra of a Hilbert algebra is also a Hilbert algebra.

Properties

Let H be the Hilbert space completion of 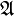$\mathfrak{A}$ with respect to the inner product and let J denote the extension of the involution to a conjugate-linear involution of H. Define a representation λ and an anti-representation ρ of 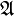$\mathfrak{A}$ on itself by left and right multiplication:

\lambda(a)x=ax,\, \, \rho(a)x=xa.

These actions extend continuously to actions on H. In this case the commutation theorem for Hilbert algebras states that

\lambda(\mathfrak{A})^{\prime\prime}=\rho(\mathfrak{A})^\prime

Moreover if

M=\lambda(\mathfrak{A})^{\prime\prime},

the von Neumann algebra generated by the operators λ(a), then

JMJ=M^\prime

These results were proved independently by Godement (1954) and Segal (1953).

The proof relies on the notion of "bounded elements" in the Hilbert space completion H.

An element of x in H is said to be bounded (relative to 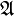$\mathfrak{A}$ ) if the map a → xa of 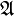$\mathfrak{A}$ into H extends to a bounded operator on H, denoted by λ(x). In this case it is straightforward to prove that:^[13]

Jx is also a bounded element, denoted x*, and λ(x*) = λ(x)*;
a → ax is given by the bounded operator ρ(x) = Jλ(x*)J on H;
M ' is generated by the ρ(x)'s with x bounded;
λ(x) and ρ(y) commute for x, y bounded.

The commutation theorem follows immediately from the last assertion. In particular

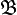M = λ( $\mathfrak{B}$ )".

The space of all bounded elements 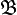$\mathfrak{B}$ forms a Hilbert algebra containing 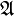$\mathfrak{A}$ as a dense *-subalgebra. It is said to be completed or full because any element in H bounded relative to 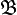$\mathfrak{B}$ must actually already lie in 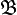$\mathfrak{B}$ . The functional τ on M₊ defined by

\tau(x) = (a,a)

if x =λ(a)*λ(a) and ∞ otherwise, yields a faithful semifinite trace on M with

M_0=\mathfrak{B}.

Thus:

There is a one-one correspondence between von Neumann algebras on H with faithful semifinite trace and full Hilbert algebras with Hilbert space completion H.

Notes

↑ 1.0 1.1 Rieffel & van Daele 1977
↑ 2.0 2.1 2.2 2.3 Dixmier 1957
↑ H₁ can be identified with the space of square integrable functions on X x Γ with respect to the product measure.
↑ It should not be confused with the von Neumann algebra on H generated by A and the operators U_g.
↑ Connes 1979
↑ 6.0 6.1 Takesaki 2002
↑ Simon 1979
↑ Dixmier uses the adjectives achevée or maximale.
↑ Pedersen 1979
↑ Bratteli & Robinson 1987
↑ Dixmier 1977, Appendix A54–A61.
↑ Dieudonné 1976
↑ Godement 1954, pp. 52–53

References

Bratteli, O.; Robinson, D.W. (1987), Operator Algebras and Quantum Statistical Mechanics 1, Second Edition, Springer-Verlag, ISBN 3-540-17093-6
Connes, A. (1979), Sur la théorie non commutative de l’intégration, Lecture Notes in Mathematics, (Algèbres d'Opérateurs), Springer-Verlag, pp. 19–143, ISBN 978-3-540-09512-5
Dieudonné, J. (1976), Treatise on Analysis, Vol. II, Academic Press, ISBN 0-12-215502-5
Dixmier, J. (1957), Les algèbres d'opérateurs dans l'espace hilbertien: algèbres de von Neumann, Gauthier-Villars
Dixmier, J. (1981), Von Neumann algebras, North Holland, ISBN 0-444-86308-7 (English translation)
Dixmier, J. (1969), Les C*-algèbres et leurs représentations, Gauthier-Villars, ISBN 0-7204-0762-1
Dixmier, J. (1977), C* algebras, North Holland, ISBN 0-7204-0762-1 (English translation)
Godement, R. (1951), "Mémoire sur la théorie des caractères dans les groupes localement compacts unimodulaires", J. Math. Pures Appl. 30: 1–110
Godement, R. (1954), "Théorie des caractères. I. Algèbres unitaires", Ann. Of Math. (Annals of Mathematics) 59 (1): 47–62, doi:10.2307/1969832, JSTOR 1969832
Murray, F.J.; von Neumann, J. (1936), "On rings of operators", Ann. Of Math. (2) (Annals of Mathematics) 37 (1): 116–229, doi:10.2307/1968693, JSTOR 1968693
Murray, F.J.; von Neumann, J. (1937), "On rings of operators II", Trans. Amer. Math. Soc. (American Mathematical Society) 41 (2): 208–248, doi:10.2307/1989620, JSTOR 1989620
Murray, F.J.; von Neumann, J. (1943), "On rings of operators IV", Ann. Of Math. (2) (Annals of Mathematics) 44 (4): 716–808, doi:10.2307/1969107, JSTOR 1969107
Pedersen, G.K. (1979), C* algebras and their automorphism groups, London Mathematical Society Monographs 14, Academic Press, ISBN 0-12-549450-5
Rieffel, M.A.; van Daele, A. (1977), "A bounded operator approach to Tomita–Takesaki theory", Pacific J. Math. 69: 187–221, doi:10.2140/pjm.1977.69.187
Segal, I.E. (1953), "A non-commutative extension of abstract integration", Ann. Of Math. (Annals of Mathematics) 57 (3): 401–457, doi:10.2307/1969729, JSTOR 1969729 (Section 5)
Simon, B. (1979), Trace ideals and their applications, London Mathematical Society Lecture Note Series 35, Cambridge University Press, ISBN 0-521-22286-9
Takesaki, M. (2002), Theory of Operator Algebras II, Springer-Verlag, ISBN 3-540-42914-X

Commutation theorem

Commutation theorem for finite traces

Examples

Commutation theorem for semifinite traces

Hilbert algebras

Definition

Examples

Properties

See also

Notes

References