Commutation matrix

In mathematics, especially in linear algebra and matrix theory, the commutation matrix is used for transforming the vectorized form of a matrix into the vectorized form of its transpose. Specifically, the commutation matrix K^(m,n) is the mn × mn matrix which, for any m × n matrix A, transforms vec(A) into vec(A^T):

K^(m,n) vec(A) = vec(A^T) .

Here vec(A) is the mn × 1 column vector obtain by stacking the columns of A on top of one another:

vec(A) = [ A_1,1, ..., A_m,1, A_1,2, ..., A_m,2, ..., A_1,n, ..., A_m,n ]^T

where A = [A_i,j].

The commutation matrix is a special type of permutation matrix, and is therefore orthogonal. Replacing A with A^T in the definition of the commutation matrix shows that K^(m,n) = (K^(n,m))^T. Therefore in the special case of m = n the commutation matrix is an involution and symmetric.

The main use of the commutation matrix, and the source of its name, is to commute the Kronecker product: for every m × n matrix A and every r × q matrix B,

K^(r,m)(A

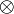\otimes

B)K^(n,q) = B

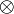\otimes

An explicit form for the commutation matrix is as follows: if e_r,j denotes the j-th canonical vector of dimension r (i.e. the vector with 1 in the j-th coordinate and 0 elsewhere) then

K^(r,m) =

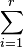
\sum_{i=1}^{r}

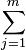\sum_{j=1}^{m}

e_r,ie_m,j^T

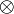\otimes

e_m,je_r,i^T.

Example

Let M be a 2x2 square matrix.

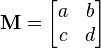
$\mathbf{M} = \begin{bmatrix} a & b \\ c & d \\ \end{bmatrix}$

Then we have

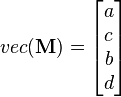
$vec(\mathbf{M}) = \begin{bmatrix} a \\ c \\ b \\ d \\ \end{bmatrix}$

And K^(2,2) is the 4x4 square matrix that will transform vec(M) into vec(M^T)

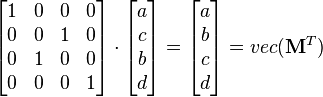
$\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0\\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} \cdot \begin{bmatrix} a \\ c \\ b \\ d \\ \end{bmatrix} = \begin{bmatrix} a \\ b \\ c \\ d \\ \end{bmatrix} = vec(\mathbf{M}^T)$

References

Jan R. Magnus and Heinz Neudecker (1988), Matrix Differential Calculus with Applications in Statistics and Econometrics, Wiley.