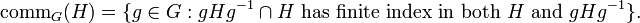Commensurator

In group theory, a branch of abstract algebra, the commensurator of a subgroup H of a group G is a specific subgroup of G.

Definition

The commensurator of a subgroup H of a group G, denoted comm_G(H) or by some comm(H),^[1] is the set of all elements g of G that conjugate H and leave the result commensurable with H. In other words

^[2]

Properties

• comm_G(H) is a subgroup of G.
• comm_G(H) = G for any compact open subgroup H.

See also

• Commensurability (mathematics)

Notes

References

• Geoghegan, Ross (2008), Topological Methods in Group Theory, Graduate Texts in Mathematics, Springer, ISBN 978-0-387-74611-1 .
• Onishchik, A.L. & Vinberg, E.B. (2000), Lie groups and Lie algebras II, Encyclopaedia of mathematical sciences, Springer, ISBN 3-540-50585-7 .