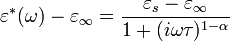Cole–Cole equation

The Cole–Cole equation is a relaxation model that is often used to describe dielectric relaxation in polymers.

It is given by the equation

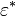\varepsilon^*(\omega) - \varepsilon_\infty = \frac{\varepsilon_s - \varepsilon_\infty}{1+(i\omega\tau)^{1 - \alpha}}

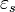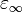where $\varepsilon^*$ is the complex dielectric constant, $\varepsilon_s$ and $\varepsilon_\infty$ are the "static" and "infinite frequency" dielectric constants, 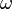$\omega$ is the angular frequency and $\tau$ is a time constant.

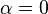The exponent parameter $\alpha$ , which takes a value between 0 and 1, allows to describe different spectral shapes. When $\alpha=0$ , the Cole-Cole model reduces to the Debye model. When 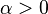$\alpha>0$ , the relaxation is stretched, i.e. it extends over a wider range on a logarithmic $\omega$ scale than Debye relaxation.

Cole-Cole relaxation constitutes a special case of Havriliak-Negami relaxation when the symmetry parameter (β) is equal to 1 - that is, when the relaxation peaks are symmetric. Another special case of Havriliak-Negami relaxation (β<1, α=0) is known as Cole-Davidson relaxation, for an abridged and updated review of anomalous dielectric relaxation in dissored systems see Kalmykov.

References

Cole, K.S.; Cole, R.H. (1941). "Dispersion and Absorption in Dielectrics - I Alternating Current Characteristics". J. Chem. Phys. 9: 341–352. Bibcode:1941JChPh...9..341C. doi:10.1063/1.1750906.

Cole, K.S.; Cole, R.H. (1942). "Dispersion and Absorption in Dielectrics - II Direct Current Characteristics". Journal of Chemical Physics 10: 98–105. Bibcode:1942JChPh..10...98C. doi:10.1063/1.1723677.

Kalmykov, Y.P.; Coffey, W.T.; Crothers, D.S.F.; Titov, S.V. (2004). "Microscopic Models for Dielectric Relaxation in Disordered Systems". Physical Review E 70: 041103. Bibcode:2004PhRvE..70d1103K. doi:10.1103/PhysRevE.70.041103.