Cohomology operation
In mathematics, the cohomology operation concept became central to algebraic topology, particularly homotopy theory, from the 1950s onwards, in the shape of the simple definition that if F is a functor defining a cohomology theory, then a cohomology operation should be a natural transformation from F to itself. Throughout there have been two basic points:
- the operations can be studied by combinatorial means; and
- the effect of the operations is to yield an interesting bicommutant theory.
The origin of these studies was the work of Pontryagin, Postnikov, and Norman Steenrod, who first defined the Pontryagin square, Postnikov square, and Steenrod square operations for singular cohomology, in the case of mod 2 coefficients. The combinatorial aspect there arises as a formulation of the failure of a natural diagonal map, at cochain level. The general theory of the Steenrod algebra of operations has been brought into close relation with that of the symmetric group.
In the Adams spectral sequence the bicommutant aspect is implicit in the use of Ext functors, the derived functors of Hom-functors; if there is a bicommutant aspect, taken over the Steenrod algebra acting, it is only at a derived level. The convergence is to groups in stable homotopy theory, about which information is hard to come by. This connection established the deep interest of the cohomology operations for homotopy theory, and has been a research topic ever since. An extraordinary cohomology theory has its own cohomology operations, and these may exhibit a richer set on constraints.
Formal definition
A cohomology operation  of type
of type
is a natural transformation of functors
defined on CW complexes.
Relation to Eilenberg-MacLane spaces
Cohomology of CW complexes is representable by an Eilenberg-MacLane space, so by the Yoneda lemma a cohomology operation of type  is given by a homotopy class of maps
is given by a homotopy class of maps  . Using representability once again, the cohomology operation is given by an element of
. Using representability once again, the cohomology operation is given by an element of 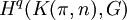 .
.
Symbolically, letting ![[A,B]](../I/m/6c05dc26810646388d97a955bb009058.png) denote the set of homotopy classes of maps from
denote the set of homotopy classes of maps from  to
to  ,
,
See also
References
- Mosher, Robert E.; Tangora, Martin C. (2008) [1968], Cohomology operations and applications in homotopy theory, New York: Dover Publications, ISBN 978-0-486-46664-4, MR 0226634
- Steenrod, N. E. (1962), Epstein, D. B. A., ed., Cohomology operations, Annals of Mathematics Studies 50, Princeton University Press, ISBN 978-0-691-07924-0, MR 0145525


![\begin{align}\displaystyle\mathrm{Nat}(H^n(-,\pi),H^q(-,G)) &= \mathrm{Nat}([-,K(\pi,n)],[-,K(G,q)])\\ &= [K(\pi,n),K(G,q)]\\ &= H^q(K(\pi,n);G).\end{align}](../I/m/ff8cbf01cefa89a86f1e6c0911cae6b8.png)