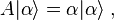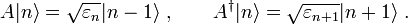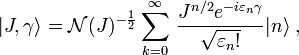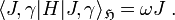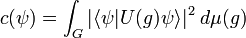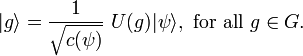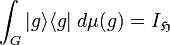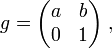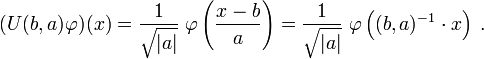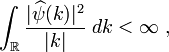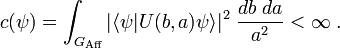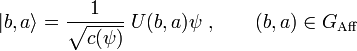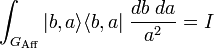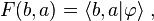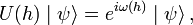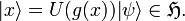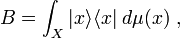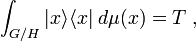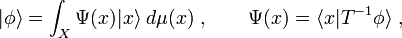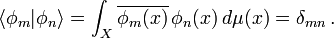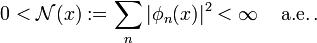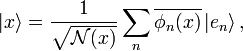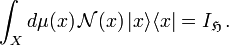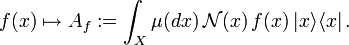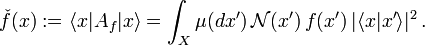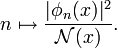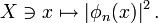Coherent states in mathematical physics
Coherent states have been introduced in a physical context, first as quasi-classical states in quantum mechanics, then as the backbone of quantum optics and they are described in that spirit in the article Coherent states (see also[1]). However, they have generated a huge variety of generalizations, which have led to a tremendous literature in mathematical physics. In this article, we will sketch the main directions of research on this line. For further details, we refer to several existing surveys .[2][3][4]
A general definition
Let 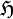 be a complex, separable Hilbert space,
be a complex, separable Hilbert space,  a locally compact space and
a locally compact space and 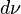 a measure on
a measure on  . For each
. For each  in
in  , denote
, denote 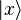 a vector in
a vector in 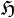 . Assume that this set of vectors possesses the following properties:
. Assume that this set of vectors possesses the following properties:
- The mapping
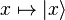 is weakly continuous, i.e., for each vector
is weakly continuous, i.e., for each vector 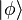 in
in 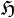 , the function
, the function 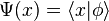 is continuous (in the topology of
is continuous (in the topology of  ).
). - The resolution of the identity
holds in the weak sense on the Hilbert space 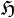 , i.e., for any two vectors
, i.e., for any two vectors 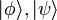 in
in 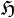 , the following equality holds:
, the following equality holds:
A set of vectors 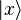 satisfying the two properties above is called a family of generalized coherent states.
In order to recover the previous definition (given in the article Coherent state) of canonical or standard coherent states (CCS), it suffices to take
satisfying the two properties above is called a family of generalized coherent states.
In order to recover the previous definition (given in the article Coherent state) of canonical or standard coherent states (CCS), it suffices to take 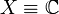 , the complex plane,
, the complex plane,  and
and 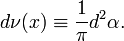
Sometimes the resolution of the identity condition is replaced by a weaker condition, with the vectors 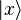 simply forming a total set in
simply forming a total set in 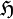 and the functions
and the functions 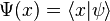 , as
, as
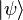 runs through
runs through 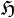 , forming a reproducing kernel Hilbert space.
The objective in both cases is to ensure that an arbitrary vector
, forming a reproducing kernel Hilbert space.
The objective in both cases is to ensure that an arbitrary vector 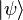 be expressible as a linear (integral) combination of these vectors. Indeed, the resolution of the identity immediately implies that
be expressible as a linear (integral) combination of these vectors. Indeed, the resolution of the identity immediately implies that
where 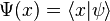 .
.
These vectors 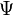 are square integrable, continuous functions on
are square integrable, continuous functions on  and satisfy the reproducing property
and satisfy the reproducing property
where 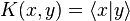 is the reproducing kernel, which satisfies the following properties
is the reproducing kernel, which satisfies the following properties
Some examples
We present in this section some of the more commonly used types of coherent states, as illustrations of the general structure given above.
Nonlinear coherent states
A large class of generalizations of the CCS is
obtained by a simple modification of their analytic structure. Let 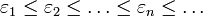 be an infinite sequence of positive numbers (
be an infinite sequence of positive numbers (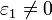 ). Define
). Define
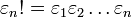 and by convention set
and by convention set 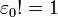 . In the same Fock space
in which the CCS were described, we now define the
related deformed or nonlinear coherent states by the expansion
. In the same Fock space
in which the CCS were described, we now define the
related deformed or nonlinear coherent states by the expansion
The normalization factor 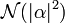 is chosen so that
is chosen so that
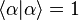 . These generalized coherent states are overcomplete
in the Fock space and satisfy a resolution of the identity
. These generalized coherent states are overcomplete
in the Fock space and satisfy a resolution of the identity
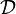 being an open disc in the complex plane of radius
being an open disc in the complex plane of radius  , the radius of convergence of the series
, the radius of convergence of the series
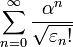 (in the case of the CCS,
(in the case of the CCS, 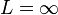 .)
The measure
.)
The measure 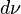 is generically of the form
is generically of the form 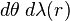 (for
(for 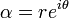 ), where
), where 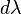 is related to the
is related to the 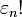 through the moment condition.
through the moment condition.
Once again, we see that for an arbitrary vector 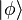 in the Fock space, the
function
in the Fock space, the
function 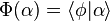 is of the form
is of the form 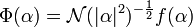 , where
, where 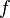 is an analytic function on the domain
is an analytic function on the domain 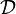 . The reproducing kernel associated to these coherent states is
. The reproducing kernel associated to these coherent states is
Barut–Girardello coherent states
By analogy with the CCS case, one can define a generalized
annihilation operator  by its action on the vectors
by its action on the vectors 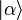 ,
,
and its adjoint operator 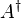 . These act on the Fock states
. These act on the Fock states 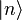 as
as
Depending on the exact values of the quantities 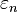 , these two operators, together
with the identity
, these two operators, together
with the identity 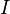 and all their commutators, could generate a wide range of algebras
including various types of deformed quantum algebras. The term 'nonlinear', as often applied to these
generalized coherent states, comes again from quantum optics where many such families of
states are used in studying the interaction between the radiation field and atoms,
where the strength of the interaction itself depends on the frequency of radiation. Of course,
these coherent states will not in general have either the group theoretical or the minimal
uncertainty properties of the CCS (there might have more general ones).
and all their commutators, could generate a wide range of algebras
including various types of deformed quantum algebras. The term 'nonlinear', as often applied to these
generalized coherent states, comes again from quantum optics where many such families of
states are used in studying the interaction between the radiation field and atoms,
where the strength of the interaction itself depends on the frequency of radiation. Of course,
these coherent states will not in general have either the group theoretical or the minimal
uncertainty properties of the CCS (there might have more general ones).
Operators  and
and 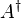 of the general type defined above
are also known as ladder operators . When such operators appear as generators of
representations of Lie algebras, the eigenvectors of
of the general type defined above
are also known as ladder operators . When such operators appear as generators of
representations of Lie algebras, the eigenvectors of  are usually called Barut–Girardello coherent states.[5]
A typical example is obtained from the representations of the Lie algebra of SU(1,1) on the Fock space.
are usually called Barut–Girardello coherent states.[5]
A typical example is obtained from the representations of the Lie algebra of SU(1,1) on the Fock space.
Gazeau–Klauder coherent states
A non-analytic extension of the above expression of the non-linear coherent states is often used to define generalized
coherent states associated to physical Hamiltonians having pure point spectra.
These coherent states, known as Gazeau-Klauder coherent states, are labelled by action-angle variables.[6]
Suppose that we are given the physical Hamiltonian 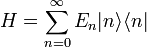 , with
, with 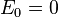 , i.e., it has the energy eigenvalues
, i.e., it has the energy eigenvalues
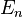 and eigenvectors
and eigenvectors 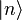 , which we assume to form an orthonormal basis for the
Hilbert space of states
, which we assume to form an orthonormal basis for the
Hilbert space of states 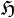 . Let us write the eigenvalues as
. Let us write the eigenvalues as
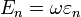 by introducing a sequence of dimensionless
quantities
by introducing a sequence of dimensionless
quantities 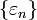 ordered as:
ordered as:
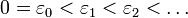 . Then, for all
. Then, for all 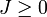 and
and
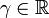 , the Gazeau–Klauder coherent states are defined as
, the Gazeau–Klauder coherent states are defined as
where again 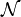 is a normalization factor, which turns out to be dependent on
is a normalization factor, which turns out to be dependent on 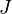 only.
These coherent states satisfy the temporal stability condition,
only.
These coherent states satisfy the temporal stability condition,
and the action identity,
While these generalized coherent states do form an overcomplete set in 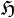 , the
resolution of the identity is generally not given by an integral relation as above, but instead by an integral in Bohr's sense,
like it is in use in the theory of almost periodic functions.[7]
, the
resolution of the identity is generally not given by an integral relation as above, but instead by an integral in Bohr's sense,
like it is in use in the theory of almost periodic functions.[7]
Actually the construction of Gazeau–Klauder CS can be extended to vector CS and to Hamiltonians with degenerate spectra, as shown by Ali and Bagarello.[8]
The group-theoretical approach
Gilmore and Perelomov, independently, realized that the construction of coherent states may sometimes be viewed as a group theoretical problem.[9][10][11][12][13][14]
In order to see this, let us go back for a while to the case of CCS.
There, indeed, the displacement operator 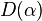 is nothing but the representative in Fock space of an element of the Heisenberg group (also called the Weyl–Heisenberg group),
whose Lie algebra is generated by
is nothing but the representative in Fock space of an element of the Heisenberg group (also called the Weyl–Heisenberg group),
whose Lie algebra is generated by 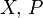 and
and 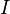 .
However, before going on with the CCS, take first the general case.
.
However, before going on with the CCS, take first the general case.
Let  be a locally compact group and suppose that it has a continuous, irreducible representation
[15]
be a locally compact group and suppose that it has a continuous, irreducible representation
[15]  on a Hilbert
space
on a Hilbert
space 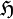 by unitary operators
by unitary operators 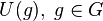 . This representation is called
square integrable if there exists a non-zero vector
. This representation is called
square integrable if there exists a non-zero vector 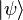 in
in 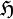 for which the integral
for which the integral
converges. Here 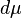 is the left invariant Haar measure on
is the left invariant Haar measure on  .
A vector
.
A vector 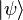 for which
for which 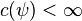 is said to be
admissible, and it can be shown that the existence of one such vector
guarantees the existence of an entire dense set of such vectors in
is said to be
admissible, and it can be shown that the existence of one such vector
guarantees the existence of an entire dense set of such vectors in 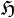 . Moreover,
if the group
. Moreover,
if the group  is unimodular, i.e., if the left and the right invariant measures
coincide, then the existence of one admissible vector implies that every vector in
is unimodular, i.e., if the left and the right invariant measures
coincide, then the existence of one admissible vector implies that every vector in
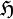 is admissible. Given a square integrable representation
is admissible. Given a square integrable representation  and an admissible vector
and an admissible vector
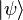 , let us define the vectors
, let us define the vectors
These vectors are the analogues of the canonical coherent states, written there in terms of the representation of the Heisenberg group (however, see the section on Gilmore-Perelomov CS, below). Next, it can be shown that the resolution of the identity
holds on 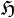 . Thus, the vectors
. Thus, the vectors 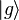 constitute a family of generalized
coherent states. The functions
constitute a family of generalized
coherent states. The functions 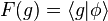 for all vectors
for all vectors
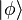 in
in 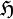 are square integrable with respect to the measure
are square integrable with respect to the measure
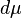 and the set of such functions, which in fact are continuous in the topology
of
and the set of such functions, which in fact are continuous in the topology
of  , forms a closed subspace of
, forms a closed subspace of 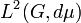 . Furthermore, the mapping
. Furthermore, the mapping
 is a linear isometry between
is a linear isometry between 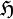 and
and 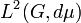 and
under this isometry the representation $U$ gets mapped to a subrepresentation of the
left regular representation of
and
under this isometry the representation $U$ gets mapped to a subrepresentation of the
left regular representation of  on
on 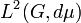 .
.
An example: wavelets
A typical example of the above construction is provided by the affine group of the line, 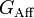 . This is the group of all 2
. This is the group of all 2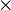 2 matrices of the type,
2 matrices of the type,
 and
and  being real numbers with
being real numbers with 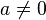 . We shall also write
. We shall also write
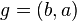 , with the action on
, with the action on 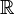 given by
given by 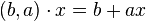 . This group is non-unimodular, with the left invariant measure being given
by
. This group is non-unimodular, with the left invariant measure being given
by 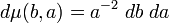 (the right invariant measure being
(the right invariant measure being 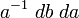 ).
The affine group has a unitary irreducible representation on the Hilbert space
).
The affine group has a unitary irreducible representation on the Hilbert space 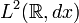 .
Vectors in
.
Vectors in 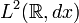 are measurable functions
are measurable functions 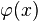 of the real variable
of the real variable  and the (unitary) operators
and the (unitary) operators 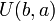 of this
representation act on them as
of this
representation act on them as
If 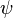 is a function in
is a function in 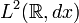 such that its Fourier transform
such that its Fourier transform
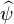 satisfies the (admissibility) condition
satisfies the (admissibility) condition
then it can be shown to be an admissible vector, i.e.,
Thus, following the general construction outlined above, the vectors
define a family of generalized coherent states and one has the resolution of the identity
on 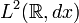 .
In the signal analysis literature, a vector satisfying the admissibility
condition above is called a mother wavelet and the generalized
coherent states
.
In the signal analysis literature, a vector satisfying the admissibility
condition above is called a mother wavelet and the generalized
coherent states 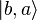 are called wavelets. Signals are then
identified with vectors
are called wavelets. Signals are then
identified with vectors 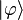 in
in 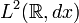 and the function
and the function
is called the continuous wavelet transform of the signal 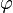 .
[16]
[17]
.
[16]
[17]
This concept can be extended to two dimensions, the group 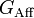 being replaced by the so-called similitude group of the plane, which consists of plane translations, rotations and global dilations.
The resulting 2D wavelets, and some generalizations of them,
are widely used in image processing.
[18]
being replaced by the so-called similitude group of the plane, which consists of plane translations, rotations and global dilations.
The resulting 2D wavelets, and some generalizations of them,
are widely used in image processing.
[18]
Gilmore–Perelomov coherent states
The construction of coherent states using group representations described above is not sufficient.
Already it cannot yield the CCS, since these are not indexed by the elements of the Heisenberg group,
but rather by points of the quotient of
the latter by its center, that quotient being precisely 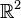 . The key observation is that the center of the Heisenberg group
leaves the vacuum vector
. The key observation is that the center of the Heisenberg group
leaves the vacuum vector 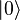 invariant, up to a phase.
Generalizing this idea, Gilmore and Perelomov
[9]
[10]
[11]
[12]
consider a locally compact group
invariant, up to a phase.
Generalizing this idea, Gilmore and Perelomov
[9]
[10]
[11]
[12]
consider a locally compact group  and a unitary irreducible
representation
and a unitary irreducible
representation  of
of  on the Hilbert space
on the Hilbert space 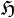 , not necessarily square integrable. Fix a vector
, not necessarily square integrable. Fix a vector 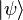 in
in 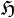 , of unit norm, and
denote by
, of unit norm, and
denote by  the subgroup of
the subgroup of  consisting of all elements
consisting of all elements 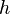 that leave it invariant up to a phase, that is,
that leave it invariant up to a phase, that is,
where 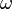 is a real-valued function of
is a real-valued function of 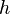 . Let
. Let 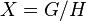 be the left coset space and
be the left coset space and
 an arbitrary element in
an arbitrary element in  . Choosing a coset representative
. Choosing a coset representative 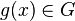 , for each coset
, for each coset  , we define the vectors
, we define the vectors
The dependence of these vectors on the specific choice of the coset representative
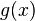 is only through a phase. Indeed, if instead of
is only through a phase. Indeed, if instead of 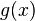 , we took a different
representative
, we took a different
representative 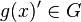 for the same coset
for the same coset  , then since
, then since 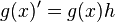 for some
for some 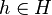 , we would have
, we would have 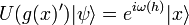 .
Hence, quantum mechanically, both
.
Hence, quantum mechanically, both 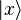 and
and
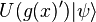 represent the same physical state and in particular, the projection operator
represent the same physical state and in particular, the projection operator
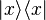 depends only on the coset. Vectors
depends only on the coset. Vectors 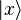 defined in this way are called
Gilmore–Perelomov coherent states. Since
defined in this way are called
Gilmore–Perelomov coherent states. Since  is assumed to be irreducible, the set of all
these vectors as
is assumed to be irreducible, the set of all
these vectors as  runs through
runs through 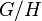 is dense in
is dense in 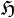 .
In this definition of generalized coherent states, no resolution of the identity is postulated. However,
if
.
In this definition of generalized coherent states, no resolution of the identity is postulated. However,
if  carries an invariant measure, under the natural action of
carries an invariant measure, under the natural action of  , and if the formal operator
, and if the formal operator  defined as
defined as
is bounded, then it is necessarily a multiple of the identity and a resolution of the identity is again retrieved.
Gilmore–Perelomov coherent states have been generalized to quantum groups, but for this we refer to the literature [19] .[20][21][22][23][24][25]
Further generalization: Coherent states on coset spaces
The Perelomov construction can be used to define coherent states for any locally compact group. On the other hand, particularly in case of failure of the Gilmore–Perelomov construction, there exist other constructions of generalized coherent states, using group representations, which generalize the notion of square integrability to homogeneous spaces of the group.[2][3]
Briefly, in this approach one starts with a unitary
irreducible representation  and attempts to find a vector
and attempts to find a vector 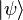 , a
subgroup
, a
subgroup  and a section
and a section 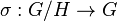 such that
such that
where 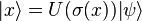 ,
, 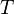 is a bounded, positive operator with bounded inverse
and
is a bounded, positive operator with bounded inverse
and 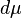 is a quasi-invariant measure on
is a quasi-invariant measure on 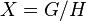 . It is not assumed that
. It is not assumed that
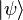 be invariant up to a phase under the action of
be invariant up to a phase under the action of  and clearly, the
best situation is when
and clearly, the
best situation is when  is a multiple of the identity. Although somewhat technical,
this general construction is of enormous versatility for semi-direct product groups of the
type
is a multiple of the identity. Although somewhat technical,
this general construction is of enormous versatility for semi-direct product groups of the
type 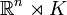 , where
, where  is a closed subgroup of
is a closed subgroup of 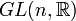 .
Thus, it is useful for many physically important groups, such as the
Poincaré group or the Euclidean group, which do not have
square integrable representations in the sense of the earlier definition.
In particular, the integral condition defining the operator
.
Thus, it is useful for many physically important groups, such as the
Poincaré group or the Euclidean group, which do not have
square integrable representations in the sense of the earlier definition.
In particular, the integral condition defining the operator  ensures that any vector
ensures that any vector
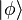 in
in 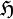 can be written in terms of the generalized coherent states
can be written in terms of the generalized coherent states 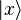 namely,
namely,
which is the primary aim of any kind of coherent states.
Coherent states: a Bayesian construction for the quantization of a measure set
We now depart from the standard situation and present a general method of construction of coherent states, starting from a few observations on the structure of these objects as
superpositions of eigenstates of some self-adjoint operator, as was the harmonic oscillator Hamiltonian for the standard CS. It is the essence of quantum mechanics that this superposition
has a probabilistic flavor. As a matter of fact, we notice that the probabilistic structure of the canonical coherent states involves two probability distributions that underlie their construction.
There are, in a sort of duality, a Poisson distribution ruling the probability of detecting  excitations when the quantum system is in a coherent state
excitations when the quantum system is in a coherent state 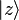 ,
and a gamma distribution on the set
,
and a gamma distribution on the set 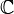 of complex parameters, more exactly on the range
of complex parameters, more exactly on the range 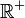 of the square of the radial variable.
The generalization follows that duality scheme.
Let
of the square of the radial variable.
The generalization follows that duality scheme.
Let  be a set of parameters equipped with a measure
be a set of parameters equipped with a measure  and its associated Hilbert space
and its associated Hilbert space 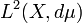 of complex-valued functions, square integrable with respect to
of complex-valued functions, square integrable with respect to  . Let us choose
in
. Let us choose
in 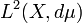 a finite or countable orthonormal set
a finite or countable orthonormal set 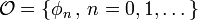 :
:
In case of infinite countability, this set must obey the (crucial) finiteness condition:
Let 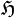 be a separable complex Hilbert space with orthonormal basis
be a separable complex Hilbert space with orthonormal basis
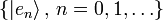 in one-to-one correspondence with the elements of
in one-to-one correspondence with the elements of 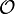 .
The two conditions above
imply that the family of normalized coherent states
.
The two conditions above
imply that the family of normalized coherent states 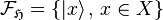 in
in 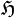 , which are defined by
, which are defined by
resolves the identity in 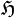 :
:
Such a relation allows us to implement a coherent state or frame quantization of the set of parameters  by associating to a function
by associating to a function 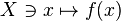 that satisfies
appropriate conditions the following operator in
that satisfies
appropriate conditions the following operator in 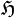 :
:
The operator 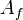 is symmetric if
is symmetric if 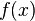 is real-valued, and it is self-adjoint (as a quadratic form) if
is real-valued, and it is self-adjoint (as a quadratic form) if 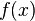 is real and semi-bounded. The original
is real and semi-bounded. The original 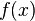 is an upper symbol, usually non-unique, for the operator
is an upper symbol, usually non-unique, for the operator 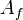 . It will be called a
classical observable with respect to the family
. It will be called a
classical observable with respect to the family 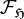 if the so-called
lower symbol of
if the so-called
lower symbol of 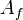 , defined as
, defined as
has mild functional properties to be made precise according to further topological properties granted to the original set  .
A last point of this construction of the space of quantum states concerns its statistical aspects.
There is indeed an interplay between two probability distributions:
.
A last point of this construction of the space of quantum states concerns its statistical aspects.
There is indeed an interplay between two probability distributions:
(i) For almost each  , a discrete distribution,
, a discrete distribution,
This probability could be considered as concerning experiments performed on the system within some experimental protocol, in order to measure the spectral values of a certain self-adjoint operator  , i.e., a quantum observable, acting in
, i.e., a quantum observable, acting in 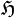 and having the discrete spectral resolution
and having the discrete spectral resolution 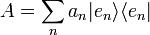 .
.
(ii) For each  , a continuous distribution on
, a continuous distribution on 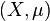 ,
,
Here, we observe a Bayesian duality typical of coherent states. There are two interpretations: the resolution of the unity verified by the coherent states 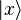 introduces a preferred prior measure on the set
introduces a preferred prior measure on the set  , which is the set of parameters of the discrete distribution, with this distribution itself playing the role of the likelihood function. The associated discretely indexed continuous distributions become the related conditional posterior distribution. Hence, a probabilistic approach to experimental observations concerning
, which is the set of parameters of the discrete distribution, with this distribution itself playing the role of the likelihood function. The associated discretely indexed continuous distributions become the related conditional posterior distribution. Hence, a probabilistic approach to experimental observations concerning  should serve as a guideline in choosing the set of the
should serve as a guideline in choosing the set of the 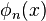 's.
We note that the continuous prior distribution will be relevant for the quantization whereas the discrete posterior one characterizes the measurement of the physical spectrum from which is built the coherent superposition of quantum states
's.
We note that the continuous prior distribution will be relevant for the quantization whereas the discrete posterior one characterizes the measurement of the physical spectrum from which is built the coherent superposition of quantum states 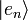 .[1]
.[1]
See also
References
- ↑ 1.0 1.1 J-P. Gazeau,Coherent States in Quantum Physics, Wiley-VCH, Berlin, 2009.
- ↑ 2.0 2.1 S.T. Ali, J-P. Antoine, J-P. Gazeau, and U.A. Mueller, Coherent states and their generalizations: A mathematical overview, Reviews in Mathematical Physics 7 (1995) 1013-1104.
- ↑ 3.0 3.1 S.T. Ali, J-P. Antoine, and J-P. Gazeau, Coherent States, Wavelets and Their Generalizations, Springer-Verlag, New York, Berlin, Heidelberg, 2000.
- ↑ S.T. Ali, Coherent States, Encyclopedia of Mathematical Physics, pp. 537-545; Elsevier, Amsterdam, 2006.
- ↑ A. O. Barut and L. Girardello, New "coherent" states associated with non compact groups, Commun. Math. Phys. 21 (1971) 41–55.
- ↑ J-P. Gazeau and J. R. Klauder, Coherent states for systems with discrete and continuous spectrum, J. Phys. A: Math. Gen. 32(1999) 123–132.
- ↑ Almost periodic function
- ↑ S. T. Ali and F. Bagarello, Some physical appearances of vector coherent states and coherent states related to degenerate Hamiltonians, J. Math. Phys. , 46 (2005) 053518.
- ↑ 9.0 9.1 A. M. Perelomov, Coherent states for arbitrary Lie groups, Commun. Math. Phys. 26 (1972) 222–236; arXiv: math-ph/0203002.
- ↑ 10.0 10.1 A. Perelomov, Generalized coherent states and their applications, Springer, Berlin 1986.
- ↑ 11.0 11.1 R. Gilmore, Geometry of symmetrized states, Ann. Phys. (NY) 74 (1972) 391–463.
- ↑ 12.0 12.1 R. Gilmore, On properties of coherent states, Rev. Mex. Fis. 23 (1974) 143–187.
- ↑ Coherent state in nLab
- ↑ E. Onofri, A note on coherent state representations of Lie groups, J. Math. Phys. 16 (1975) 1087–1089.
- ↑ Group representation
- ↑ I. Daubechies, Ten Lectures on Wavelets, SIAM, Philadelphia, 1992.
- ↑ S. G. Mallat, A Wavelet Tour of Signal Processing, 2nd ed., Academic Press, San Diego, 1999.
- ↑ J-P. Antoine, R. Murenzi, P. Vandergheynst, and S.T. Ali, Two-Dimensional Wavelets and their Relatives, Cambridge University Press, Cambridge (UK), 2004.
- ↑ Quantum group
- ↑ L. C. Biedenharn, The quantum group
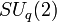 and a
and a  -analogue of the boson operators, J. Phys. A: Math. Gen. 22 (1989) L873-L878.
-analogue of the boson operators, J. Phys. A: Math. Gen. 22 (1989) L873-L878. - ↑ B. Jurčo, On coherent states for the simplest quantum groups, Lett. Math. Phys. 21 (1991) 51-58.
- ↑ E. Celeghini, M. Rasetti, and G. Vitiello, Squeezing and quantum groups, Phys. Rev. Lett. 66 (1991) 2056–2059.
- ↑ H. Sazdjian, Y.S. Stanev, I.T. Todorov, SU(3)-coherent state operators and invariant correlation functions and their quantum group counterparts, J. Math. Phys. 36 (1995) 2030-2052.
- ↑ B. Jurčo, P. Štoviček, Coherent states for quantum compact groups, Commun. Math. Phys. 182 (1996) 221-251; http://arXiv.org/abs/hep-th/9403114.
- ↑ Z. Škoda, Coherent states for Hopf algebras, Lett. Math. Phys. 81 (2007) 1; earlier version: http://arXiv.org/abs/math/0303357.
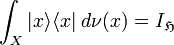
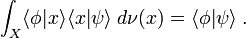
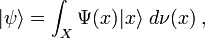
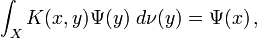
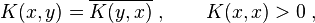
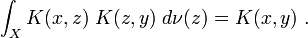
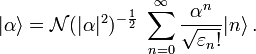
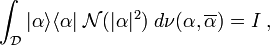
![K(\overline{\alpha}, \alpha' ) = \langle \alpha| \alpha'\rangle =
\left[{\mathcal N}(\vert \alpha\vert^2) {\mathcal N}(\vert \alpha'\vert^2)\right]^{-\frac 12}
\sum_{n=0}^\infty \frac {(\overline{\alpha} \alpha')^n}{\varepsilon_n!}\; .](../I/m/ab1b945f3dc58af02553e1657783d98b.png)