Cograph

In graph theory, a cograph, or complement-reducible graph, or P4-free graph, is a graph that can be generated from the single-vertex graph K1 by complementation and disjoint union. That is, the family of cographs is the smallest class of graphs that includes K1 and is closed under complementation and disjoint union.
Cographs have been discovered independently by several authors since the 1970s; early references include Jung (1978), Lerchs (1971), Seinsche (1974), and Sumner (1974). They have also been called D*-graphs (Jung 1978), hereditary Dacey graphs (after the related work of James C. Dacey, Jr. on orthomodular lattices; see Sumner 1974), and 2-parity graphs (Burlet & Uhry 1984).
See, e.g., Brandstädt, Le & Spinrad (1999) for more detailed coverage of cographs, including the facts presented here.
Definition and characterization
Any cograph may be constructed using the following rules:
- any single vertex graph is a cograph;
- if
 is a cograph, so is its complement
is a cograph, so is its complement 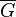 ;
; - if
 and
and  are cographs, so is their disjoint union
are cographs, so is their disjoint union 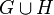 .
.
Several alternative characterizations of cographs can be given. Among them:
- A cograph is a graph which does not contain the path P4 on 4 vertices (and hence of length 3) as an induced subgraph. That is, a graph is a cograph if and only if for any four vertices
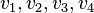 , if
, if 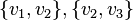 and
and 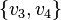 are edges of the graph then at least one of
are edges of the graph then at least one of 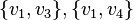 or
or 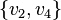 is also an edge (Corneil, Lerchs & Stewart Burlingham 1981).
is also an edge (Corneil, Lerchs & Stewart Burlingham 1981). - A cograph is a graph all of whose induced subgraphs have the property that any maximal clique intersects any maximal independent set in a single vertex.
- A cograph is a graph in which every nontrivial induced subgraph has at least two vertices with the same neighbourhoods.
- A cograph is a graph in which every connected induced subgraph has a disconnected complement.
- A cograph is a graph all of whose connected induced subgraphs have diameter at most 2.
- A cograph is a graph in which every connected component is a distance-hereditary graph with diameter at most 2.
- A cograph is a graph with clique-width at most 2 (Courcelle & Olariu 2000).
- A cograph is a comparability graph of a series-parallel partial order (Jung 1978).
- A cograph is a permutation graph of a separable permutation (Bose, Buss & Lubiw 1998).
All complete graphs, complete bipartite graphs, threshold graphs, and Turán graphs are cographs. Every cograph is distance-hereditary, a comparability graph, and perfect.
Cotrees
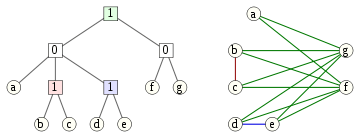
A cotree is a tree in which the internal nodes are labeled with the numbers 0 and 1. Every cotree T defines a cograph G having the leaves of T as vertices, and in which the subtree rooted at each node of T corresponds to the induced subgraph in G defined by the set of leaves descending from that node:
- A subtree consisting of a single leaf node corresponds to an induced subgraph with a single vertex.
- A subtree rooted at a node labeled 0 corresponds to the union of the subgraphs defined by the children of that node.
- A subtree rooted at a node labeled 1 corresponds to the join of the subgraphs defined by the children of that node; that is, we form the union and add an edge between every two vertices corresponding to leaves in different subtrees. Alternatively, the join of a set of graphs can be viewed as formed by complementing each graph, forming the union of the complements, and then complementing the resulting union.
An equivalent way of describing the cograph formed from a cotree is that two vertices are connected by an edge if and only if the lowest common ancestor of the corresponding leaves is labeled by 1. Conversely, every cograph can be represented in this way by a cotree. If we require the labels on any root-leaf path of this tree to alternate between 0 and 1, this representation is unique (Corneil, Lerchs & Stewart Burlingham 1981).
Computational properties
Cographs may be recognized in linear time, and a cotree representation constructed, using modular decomposition (Corneil, Perl & Stewart 1985), partition refinement (Habib & Paul 2005), or split decomposition (Gioan & Paul 2008). Once a cotree representation has been constructed, many familiar graph problems may be solved via simple bottom-up calculations on the cotrees.
For instance, to find the maximum clique in a cograph, compute in bottom-up order the maximum clique in each subgraph represented by a subtree of the cotree. For a node labeled 0, the maximum clique is the maximum among the cliques computed for that node's children. For a node labeled 1, the maximum clique is the union of the cliques computed for that node's children, and has size equal to the sum of the children's clique sizes. Thus, by alternately maximizing and summing values stored at each node of the cotree, we may compute the maximum clique size, and by alternately maximizing and taking unions, we may construct the maximum clique itself. Similar bottom-up tree computations allow the maximum independent set, vertex coloring number, maximum clique cover, and Hamiltonicity (that is the existence of a Hamiltonian cycle) to be computed in linear time from a cotree representation of a cograph. One can also use cotrees to determine in linear time whether two cographs are isomorphic.
If H is an induced subgraph of a cograph G, then H is itself a cograph; the cotree for H may be formed by removing some of the leaves from the cotree for G and then suppressing nodes that have only one child. It follows from Kruskal's tree theorem that the relation of being an induced subgraph is a well-quasi-ordering on the cographs (Damaschke 1990). Thus, if a subfamily of the cographs (such as the planar cographs) is closed under induced subgraph operations then it has a finite number of forbidden induced subgraphs. Computationally, this means that testing membership in such a subfamily may be performed in linear time, by using a bottom-up computation on the cotree of a given graph to test whether it contains any of these forbidden subgraphs.
References
- Bose, Prosenjit; Buss, Jonathan; Lubiw, Anna (1998), "Pattern matching for permutations", Information Processing Letters 65: 277–283, doi:10.1016/S0020-0190(97)00209-3, MR 1620935.
- Brandstädt, Andreas; Le, Van Bang; Spinrad, Jeremy P. (1999), Graph Classes: A Survey, SIAM Monographs on Discrete Mathematics and Applications, ISBN 978-0-89871-432-6.
- Burlet, M.; Uhry, J. P. (1984), "Parity Graphs", Topics on Perfect Graphs, Annals of Discrete Mathematics 21, pp. 253–277.
- Corneil, D. G.; Lerchs, H.; Stewart Burlingham, L. (1981), "Complement reducible graphs", Discrete Applied Mathematics 3 (3): 163–174, doi:10.1016/0166-218X(81)90013-5, MR 0619603.
- Corneil, D. G.; Perl, Y.; Stewart, L. K. (1985), "A linear recognition algorithm for cographs", SIAM Journal on Computing 14 (4): 926–934, doi:10.1137/0214065, MR 0807891.
- Courcelle, B.; Olariu, S. (2000), "Upper bounds to the clique width of graphs", Discrete Applied Mathematics 101 (1–3): 77–144, doi:10.1016/S0166-218X(99)00184-5.
- Damaschke, Peter (1990), "Induced subgraphs and well-quasi-ordering", Journal of Graph Theory 14 (4): 427–435, doi:10.1002/jgt.3190140406, MR 1067237.
- Gioan, Emeric; Paul, Christophe (2008), Split decomposition and graph-labelled trees: characterizations and fully-dynamic algorithms for totally decomposable graphs, arXiv:0810.1823.
- Habib, Michel; Paul, Christophe (2005), "A simple linear time algorithm for cograph recognition", Discrete Applied Mathematics 145 (2): 183–197, doi:10.1016/j.dam.2004.01.011, MR 2113140.
- Jung, H. A. (1978), "On a class of posets and the corresponding comparability graphs", Journal of Combinatorial Theory, Series B 24 (2): 125–133, doi:10.1016/0095-8956(78)90013-8, MR 0491356.
- Lerchs, H. (1971), On cliques and kernels, Tech. Report, Dept. of Comp. Sci., Univ. of Toronto.
- Seinsche, D. (1974), "On a property of the class of n-colorable graphs", Journal of Combinatorial Theory, Series B 16 (2): 191–193, doi:10.1016/0095-8956(74)90063-X, MR 0337679.
- Sumner, D. P. (1974), "Dacey graphs", J. Austral. Math. Soc. 18 (04): 492–502, doi:10.1017/S1446788700029232, MR 0382082.