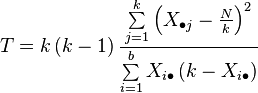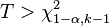Cochran's Q test

In statistics, in the analysis of two-way randomized block designs where the response variable can take only two possible outcomes (coded as 0 and 1), Cochran's Q test is a non-parametric statistical test to verify whether k treatments have identical effects.^[1]^[2]^[3] It is named for William Gemmell Cochran. Cochran's Q test should not be confused with Cochran's C test, which is a variance outlier test.

Background

Cochran's Q test assumes that there are k > 2 experimental treatments and that the observations are arranged in b blocks; that is,

	Treatment 1	Treatment 2	$\cdots$	Treatment k
Block 1	X₁₁	X₁₂	$\cdots$	X_1k
Block 2	X₂₁	X₂₂	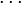$\cdots$	X_2k
Block 3	X₃₁	X₃₂	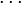$\cdots$	X_3k
$\vdots$	$\vdots$	$\vdots$	$\ddots$	$\vdots$
Block b	X_b1	X_b2	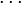$\cdots$	X_bk

Description

Cochran's Q test is

H₀: The treatments are equally effective.

H_a: There is a difference in effectiveness among treatments.

The Cochran's Q test statistic is

T = k\left(k-1\right)\frac{\sum\limits_{j=1}^k \left(X_{\bullet j} - \frac{N}{k}\right)^2}{\sum\limits_{i=1}^b X_{i\bullet}\left(k-X_{i\bullet}\right)}

where

k is the number of treatments

X_• j is the column total for the j^th treatment

b is the number of blocks

X_i • is the row total for the i^th block

N is the grand total

Critical region

For significance level α, the critical region is

T > \chi^2_{1-\alpha,k-1}

where Χ²_{1 − α,k − 1} is the (1 − α)-quantile of the chi-squared distribution with k − 1 degrees of freedom. The null hypothesis is rejected if the test statistic is in the critical region. If the Cochran test rejects the null hypothesis of equally effective treatments, pairwise multiple comparisons can be made by applying Cochran's Q test on the two treatments of interest.

Assumptions

Cochran's Q test is based on the following assumptions:

A large sample approximation; in particular, it assumes that b is "large".
The blocks were randomly selected from the population of all possible blocks.
The outcomes of the treatments can be coded as binary responses (i.e., a "0" or "1") in a way that is common to all treatments within each block.

Related tests

When using this kind of design for a response that is not binary but rather ordinal or continuous, one instead uses the Friedman test or Durbin tests.
The case where there are exactly two treatments is equivalent to McNemar's test, which is itself equivalent to a two-tailed sign test.

References

↑ William G. Cochran (December 1950). "The Comparison of Percentages in Matched Samples". Biometrika 37 (3/4): 256–266. doi:10.1093/biomet/37.3-4.256. JSTOR http://www.jstor.org/stable/2332378.
↑ Conover, William Jay (1999). Practical Nonparametric Statistics (Third Edition ed.). Wiley, New York, NY USA. pp. 388–395. ISBN 9780471160687.
↑ National Institute of Standards and Technology. Cochran Test

This article incorporates public domain material from websites or documents of the National Institute of Standards and Technology.