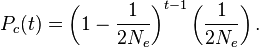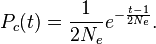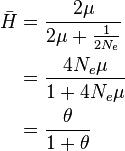Coalescent theory

In genetics, coalescent theory is a retrospective stochastic model of population genetics. It attempts to trace all alleles of a gene shared by all members of a population to a single ancestral copy, known as the most recent common ancestor (MRCA; sometimes also termed the coancestor to emphasize the coalescent relationship). The inheritance relationships between alleles are typically represented as a gene genealogy, similar in form to a phylogenetic tree. This gene genealogy is also known as the coalescent. Understanding the statistical properties of the coalescent under different assumptions forms the basis of coalescent theory.

The coalescent runs models of genetic drift backward in time to investigate the genealogy of antecedents. In the simplest case, coalescent theory assumes no recombination, no natural selection, and no gene flow or population structure. Advances in coalescent theory, however, allow extension to the basic coalescent, and can include recombination, selection, and virtually any arbitrarily complex evolutionary or demographic model in population genetic analysis. The mathematical theory of the coalescent was originally developed in the early 1980s by John Kingman.

Theory

Consider two distinct haploid organisms who differ at a single nucleotide. By tracing the ancestry of these two individuals backwards there will be a point in time when the MRCA is encountered and the two lineages will have coalesced.

Time to coalescence

A useful analysis based on coalescent theory seeks to predict the amount of time elapsed between the introduction of a mutation and the arising of a particular allele or gene distribution in a population. This time period is equal to how long ago the most recent common ancestor existed.

The probability that two lineages coalesce in the immediately preceding generation is the probability that they share a parental DNA sequence. In a diploid population with a constant effective population size with 2Ne copies of each locus, there are 2Ne "potential parents" in the previous generation. Under a random mating model, the probability that two alleles share a parent is thus 1/(2Ne) and, correspondingly, the probability that they do not coalesce is 1 − 1/(2Ne).

At each successive preceding generation, the probability of coalescence is geometrically distributed — that is, it is the probability of noncoalescence at the t − 1 preceding generations multiplied by the probability of coalescence at the generation of interest:

P_c(t) = \left( 1 - \frac{1}{2N_e} \right)^{t-1} \left(\frac{1}{2N_e}\right).

For sufficiently large values of Ne, this distribution is well approximated by the continuously defined exponential distribution

P_{c}(t) = \frac{1}{2N_e} e^{-\frac{t-1}{2N_e}}.

The standard exponential distribution has both the expected value and the standard deviation equal to 2Ne; therefore, although the expected time to coalescence is 2Ne, actual coalescence times have a wide range of variation. Note that coalescent time is the number of preceding generations where the coalescence took place and not calendar time though an estimation of the latter can be made multiplying 2Ne with the average time between generations.

Neutral variation

Coalescent theory can also be used to model the amount of variation in DNA sequences expected from genetic drift and mutation. This value is termed the mean heterozygosity, represented as 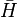\bar{H}. Mean heterozygosity is calculated as the probability of a mutation occurring at a given generation divided by the probability of any "event" at that generation (either a mutation or a coalescence). The probability that the event is a mutation is the probability of a mutation in either of the two lineages: 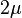2\mu. Thus the mean heterozygosity is equal to

\begin{align} \bar{H} &= \frac{2\mu}{2\mu + \frac{1}{2N_e}} \\ &= \frac{4N_e\mu}{1+4N_e\mu} \\ &= \frac{\theta}{1+\theta} \end{align}

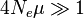For 4N_e\mu \gg 1, the vast majority of allele pairs have at least one difference in nucleotide sequence.

Graphical representation

Coalescents can be visualised using dendrograms which show the relationship of branches of the population to each other. The point where two branches meet indicates a coalescent event.

Applications

Disease gene mapping

The utility of coalescent theory in the mapping of disease is slowly gaining more appreciation; although the application of the theory is still in its infancy, there are a number of researchers who are actively developing algorithms for the analysis of human genetic data that utilise coalescent theory.

The genomic distribution of heterozygosity

The human single-nucleotide polymorphism (SNP) map has revealed large regional variations in heterozygosity, more so than can be explained on the basis of (Poisson-distributed) random chance. In part, these variations could be explained on the basis of assessment methods, the availability of genomic sequences, and possibly the standard coalescent population genetic model. Population genetic influences could have a major influence on this variation: some loci presumably would have comparatively recent common ancestors, others might have much older genealogies, and so the regional accumulation of SNPs over time could be quite different. The local density of SNPs along chromosomes appears to cluster in accordance with a variance to mean power law and to obey the Tweedie compound Poisson distribution. In this model the regional variations in the SNP map would be explained by the accumulation of multiple small genomic segments through recombination, where the mean number of SNPs per segment would be gamma distributed in proportion to a gamma distributed time to the most recent common ancestor for each segment.

History

Coalescent theory is a natural extension of the more classical population genetics concept of neutral evolution and is an approximation to the Fisher–Wright (or Wright–Fisher) model for large populations. It was discovered independently by several researchers in the 1980s.

Software

A large body of software exists for both simulating data sets under the coalescent process as well as inferring parameters such as population size and migration rates from genetic data.

References and notes

Articles

  • ^ Arenas, M. and Posada, D. (2007) Recodon: Coalescent simulation of coding DNA sequences with recombination, migration and demography. BMC Bioinformatics 8: 458
  • ^ Arenas, M. and Posada, D. (2010) Coalescent simulation of intracodon recombination. Genetics 184(2): 429–437
  • ^ Browning, S.R. (2006) Multilocus association mapping using variable-length markov chains. American Journal of Human Genetics 78:903–913
  • ^ Cornuet J.-M., Pudlo P., Veyssier J., Dehne-Garcia A., Gautier M., Leblois R., Marin J.-M., Estoup A. (2014) DIYABC v2.0: a software to make Approximate Bayesian Computation inferences about population history using Single Nucleotide Polymorphism, DNA sequence and microsatellite data. Bioinformatics '30': 1187–1189
  • ^ Degnan, JH and LA Salter. 2005. Gene tree distributions under the coalescent process. Evolution 59(1): 24–37. pdf from coaltree.net/
  • ^ Donnelly, P., Tavaré, S. (1995) Coalescents and genealogical structure under neutrality. Annual Review of Genetics 29:401–421
  • ^ Ewing, G. and Hermisson J. (2010), MSMS: a coalescent simulation program including recombination, demographic structure and selection at a single locus, Bioinformatics 26:15
  • ^ Hellenthal, G., Stephens M. (2006) msHOT: modifying Hudson's ms simulator to incorporate crossover and gene conversion hotspots Bioinformatics AOP
  • ^ Hudson RR (1983a) Testing the constant-rate neutral allele model with protein sequence data. Evolution 37: 203–207 JSTOR copy
  • ^ Hudson RR (1983b) Properties of a neutral allele model with intragenic recombination. Theoretical Population Biology 23:183–201.
  • ^ Hudson RR (1991) Gene genealogies and the coalescent process. Oxford Surveys in Evolutionary Biology 7: 1–44
  • ^ Hudson RR (2002) Generating samples under a Wright–Fisher neutral model. Bioinformatics 18:337–338
  • ^ Kendal WS (2003) An exponential dispersion model for the distribution of human single nucleotide polymorphisms. Mol Biol Evol 20: 579–590
  • Hein, J., Schierup, M., Wiuf C. (2004) Gene Genealogies, Variation and Evolution: A Primer in Coalescent Theory Oxford University Press ISBN 978-0-19-852996-5
  • ^ Kaplan, N.L., Darden, T., Hudson, R.R. (1988) The coalescent process in models with selection. Genetics 120:819–829
  • ^ Kingman, J.F.C. (1982) On the Genealogy of Large Populations. Journal of Applied Probability 19A:27–43 JSTOR copy
  • ^ Kingman, J.F.C. (2000) Origins of the coalescent 1974–1982. Genetics 156:1461–1463
  • ^ Leblois R., Estoup A. and Rousset F. (2009) IBDSim: a computer program to simulate genotypic data under isolation by distance Molecular Ecology Resources 9:107–109
  • ^ Liang L., Zöllner S., Abecasis G.R. (2007) GENOME: a rapid coalescent-based whole genome simulator. Bioinformatics 23: 1565–1567
  • ^ Mailund, T., Schierup, M.H., Pedersen, C.N.S., Mechlenborg, P. J. M., Madsen, J.N., Schauser, L. (2005) CoaSim: A Flexible Environment for Simulating Genetic Data under Coalescent Models BMC Bioinformatics 6:252
  • ^ Möhle, M., Sagitov, S. (2001) A classification of coalescent processes for haploid exchangeable population models The Annals of Probability 29:1547–1562
  • ^ Morris, A. P., Whittaker, J. C., Balding, D. J. (2002) Fine-scale mapping of disease loci via shattered coalescent modeling of genealogies American Journal of Human Genetics 70:686–707
  • ^ Neuhauser, C., Krone, S.M. (1997) The genealogy of samples in models with selection Genetics 145 519–534
  • ^ Pitman, J. (1999) Coalescents with multiple collisions The Annals of Probability 27:1870–1902
  • ^ Harding, Rosalind, M. 1998. New phylogenies: an introductory look at the coalescent. pp. 15–22, in Harvey, P. H., Brown, A. J. L., Smith, J. M., Nee, S. New uses for new phylogenies. Oxford University Press (ISBN 0198549849)
  • ^ Rosenberg, N.A., Nordborg, M. (2002) Genealogical Trees, Coalescent Theory and the Analysis of Genetic Polymorphisms. Nature Reviews Genetics 3:380–390
  • ^ Sagitov, S. (1999) The general coalescent with asynchronous mergers of ancestral lines Journal of Applied Probability 36:1116–1125
  • ^ Schweinsberg, J. (2000) Coalescents with simultaneous multiple collisions Electronic Journal of Probability 5:1–50
  • ^ Slatkin, M. (2001) Simulating genealogies of selected alleles in populations of variable size Genetic Research 145:519–534
  • ^ Tajima, F. (1983) Evolutionary Relationship of DNA Sequences in finite populations. Genetics 105:437–460
  • ^ Tavare S, Balding DJ, Griffiths RC & Donnelly P. 1997. Inferring coalescent times from DNA sequence data. Genetics 145: 505–518.
  • ^ The international SNP map working group. 2001. A map of human genome variation containing 1.42 million single nucleotide polymorphisms. Nature 409: 928–933.
  • ^ Zöllner S. and Pritchard J.K. (2005) Coalescent-Based Association Mapping and Fine Mapping of Complex Trait Loci Genetics 169:1071–1092
  • ^ Rousset F. and Leblois R. (2007) Likelihood and Approximate Likelihood Analyses of Genetic Structure in a Linear Habitat: Performance and Robustness to Model Mis-Specification Molecular Biology and Evolution 24:2730–2745

Books

  • Hein, J; Schierup, M. H., and Wiuf, C. Gene Genealogies, Variation and Evolution – A Primer in Coalescent Theory. Oxford University Press, 2005. ISBN 0-19-852996-1.
  • Nordborg, M. (2001) Introduction to Coalescent Theory
  • Chapter 7 in Balding, D., Bishop, M., Cannings, C., editors, Handbook of Statistical Genetics. Wiley ISBN 978-0-471-86094-5
  • Wakeley J. (2006) An Introduction to Coalescent Theory Roberts & Co ISBN 0-9747077-5-9 Accompanying website with sample chapters
  • ^ Rice SH. (2004). Evolutionary Theory: Mathematical and Conceptual Foundations. Sinauer Associates: Sunderland, MA. See esp. ch. 3 for detailed derivations.
  • Berestycki N. "Recent progress in coalescent theory" 2009 ENSAIOS Matematicos vol.16
  • Bertoin J. "Random Fragmentation and Coagulation Processes"., 2006. Cambridge Studies in Advanced Mathematics, 102. Cambridge University Press, Cambridge, 2006. ISBN 978-0-521-86728-3;
  • Pitman J. "Combinatorial stochastic processes" Springer (2003)

External links