Closed convex function

In mathematics, a function 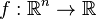$f: \mathbb{R}^n \rightarrow \mathbb{R}$ is said to be closed if for each 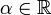$\alpha \in \mathbb{R}$ , the sublevel set 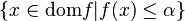$\{ x \in \mbox{dom} f \vert f(x) \leq \alpha \}$ is a closed set.

Equivalently, if the epigraph defined by 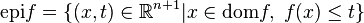$\mbox{epi} f = \{ (x,t) \in \mathbb{R}^{n+1} \vert x \in \mbox{dom} f,\; f(x) \leq t\}$ is closed, then the function 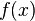$f(x)$ is closed.

This definition is valid for any function, but most used for convex function. A proper convex function is closed if and only if it is lower semi-continuous. For a convex function which is not proper there is disagreement as to the definition of the closure of the function.

Properties

If 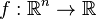$f: \mathbb{R}^n \rightarrow \mathbb{R}$ is a continuous function and 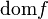$\mbox{dom} f$ is closed, then $f$ is closed.

A closed proper convex function f is the pointwise supremum of the collection of all affine functions h such that h ≤ f (called the affine minorants of f).

References

Boyd, Lieven Vandenberghe and Stephen (2004). Convex optimization. New York: Cambridge. pp. 639–640. ISBN 978-0521833783.
Rockafellar, R. Tyrrell (1997) [1970]. Convex Analysis. Princeton, NJ: Princeton University Press. ISBN 978-0-691-01586-6.