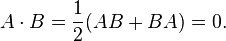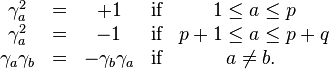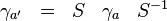Clifford module
In mathematics, a Clifford module is a representation of a Clifford algebra. In general a Clifford algebra C is a central simple algebra over some field extension L of the field K over which the quadratic form Q defining C is defined.
The abstract theory of Clifford modules was founded by a paper of M. F. Atiyah, R. Bott and Arnold S. Shapiro. A fundamental result on Clifford modules is that the Morita equivalence class of a Clifford algebra (the equivalence class of the category of Clifford modules over it) depends only on the signature p − q (mod 8). This is an algebraic form of Bott periodicity.
Matrix representations of real Clifford algebras
We will need to study anticommuting matrices (AB = −BA) because in Clifford algebras orthogonal vectors anticommute
For the real Clifford algebra 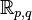 , we need p + q mutually anticommuting matrices, of which p have +1 as square and q have −1 as square.
, we need p + q mutually anticommuting matrices, of which p have +1 as square and q have −1 as square.
Such a basis of gamma matrices is not unique. One can always obtain another set of gamma matrices satisfying the same Clifford algebra by means of a similarity transformation.
where S is a non-singular matrix. The sets γ a' and γ a belong to the same equivalence class.
Real Clifford algebra R3,1
Developed by Ettore Majorana, this Clifford module enables the construction of a Dirac-like equation without complex numbers, and its elements are called Majorana spinors.
The four basis vectors are the three Pauli matrices and a fourth antihermitian matrix. The signature is (+++−). For the signatures (+−−−) and (−−−+) often used in physics, 4×4 complex matrices or 8×8 real matrices are needed.
See also
References
- Atiyah, Michael; Bott, Raoul; Shapiro, Arnold (1964), "Clifford Modules", Topology 3 ((Suppl. 1)): 3–38, doi:10.1016/0040-9383(64)90003-5
- Deligne, Pierre (1999), "Notes on spinors", in P. Deligne, P. Etingof, D. S. Freed, L. C. Jeffrey, D. Kazhdan, J. W. Morgan, D. R. Morrison, E. Witten, Quantum Fields and Strings: A Course for Mathematicians, Providence: American Mathematical Society, pp. 99–135. See also the programme website for a preliminary version.
- Harvey, F. Reese (1990), Spinors and Calibrations, Academic Press, ISBN 978-0-12-329650-4.
- Lawson, H. Blaine; Michelsohn, Marie-Louise (1989), Spin Geometry, Princeton University Press, ISBN 0-691-08542-0.