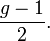Clifford's theorem on special divisors

In mathematics, Clifford's theorem on special divisors is a result of W. K. Clifford (1878) on algebraic curves, showing the constraints on special linear systems on a curve C.

Statement

If D is a divisor on C, then D is (abstractly) a formal sum of points P on C (with integer coefficients), and in this application a set of constraints to be applied to functions on C (if C is a Riemann surface, these are meromorphic functions, and in general lie in the function field of C). Functions in this sense have a divisor of zeros and poles, counted with multiplicity; a divisor D is here of interest as a set of constraints on functions, insisting that poles at given points are only as bad as the positive coefficients in D indicate, and that zeros at points in D with a negative coefficient have at least that multiplicity. The dimension of the vector space

L(D)

of such functions is finite, and denoted ℓ(D). Conventionally the linear system of divisors attached to D is then attributed dimension r(D) = ℓ(D) − 1, which is the dimension of the projective space parametrizing it.

The other significant invariant of D is its degree, d, which is the sum of all its coefficients.

A divisor is called special if ℓ(K − D) > 0, where K is the canonical divisor.^[1]

In this notation, Clifford's theorem is the statement that for an effective special divisor D,

ℓ(D) − 1 ≤ d/2,

together with the information that the case of equality here is only for D zero or canonical, or C a hyperelliptic curve and D linearly equivalent to an integral multiple of a hyperelliptic divisor.

Clifford index

The Clifford index of C is then defined as the minimum value of the d − 2r(D), taken over all special divisors. Clifford's theorem is then the statement that this is non-negative. The Clifford index for a generic curve of genus g is the floor function of

\frac{g-1}{2}.

The Clifford index measures how far the curve is from being hyperelliptic. It may be thought of as a refinement of the gonality: in many cases the Clifford index is equal to the gonality minus 2.^[2]

Green's Conjecture

A conjecture of Mark Green states that the Clifford index for a curve over the complex numbers that is not hyperelliptic should be determined by the extent to which C as canonical curve has linear syzygies. In detail, the invariant a(C) is determined by the minimal free resolution of the homogeneous coordinate ring of C in its canonical embedding, as the largest index i for which the graded Betti number β_{i, i + 2} is zero. Green and Lazarsfeld showed that a(C) + 1 is a lower bound for the Clifford index, and Green's conjecture is that equality always holds. There are numerous partial results.^[3]

Claire Voisin was awarded the Ruth Lyttle Satter Prize in Mathematics for her solution of the generic case of Green's conjecture in two papers.^[4]^[5] The case of Green's conjecture for generic curves had attracted a huge amount of effort by algebraic geometers over twenty years before finally being laid to rest by Voisin.^[6] The conjecture for arbitrary curves remains open.

Notes

↑ Hartshorne p.296
↑ Eisenbud (2005) p.178
↑ Eisenbud (2005) pp. 183-4.
↑ Green's canonical syzygy conjecture for generic curves of odd genus - Claire Voisin
↑ Green’s generic syzygy conjecture for curves of even genus lying on a K3 surface - Claire Voisin
↑ Satter Prize

References

E. Arbarello; M. Cornalba, P.A. Griffiths, J. Harris (1985). Geometry of Algebraic Curves Volume I. Grundlehren de mathematischen Wisenschaften 267. ISBN 0-387-90997-4.
Clifford, W. K. (1878), "On the Classification of Loci", Philosophical Transactions of the Royal Society of London (The Royal Society) 169: 663–681, doi:10.1098/rstl.1878.0020, ISSN 0080-4614, JSTOR 109316
Eisenbud, David (2005). The Geometry of Syzygies. A second course in commutative algebra and algebraic geometry. Graduate Texts in Mathematics 229. New York, NY: Springer-Verlag. ISBN 0-387-22215-4. Zbl 1066.14001.
William Fulton (1974). Algebraic Curves. Mathematics Lecture Note Series. W.A. Benjamin. p. 212. ISBN 0-8053-3080-1.
P.A. Griffiths; J. Harris (1994). Principles of Algebraic Geometry. Wiley Classics Library. Wiley Interscience. p. 251. ISBN 0-471-05059-8.
Robin Hartshorne (1977). Algebraic Geometry. Graduate Texts in Mathematics 52. ISBN 0-387-90244-9.

External links

Iskovskikh, V.A. (2001), "Clifford theorem", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4

Topics in algebraic curves

Rational curves

Elliptic curves

Analytic theory	Elliptic function Elliptic integral Fundamental pair of periods Modular form

Arithmetic theory	Counting points on elliptic curves Division polynomials Hasse's theorem on elliptic curves Mazur's torsion theorem Modular elliptic curve Modularity theorem Mordell–Weil theorem Nagell–Lutz theorem Supersingular elliptic curve Schoof's algorithm Schoof–Elkies–Atkin algorithm

Applications	Elliptic curve cryptography Elliptic curve primality

Higher genus

Plane curves

Riemann surfaces

Constructions

Structure of curves

Divisors on curves	Abel–Jacobi map Brill–Noether theory Clifford's theorem on special divisors Gonality of an algebraic curve Jacobian variety Riemann–Roch theorem Weierstrass point Weil reciprocity law

Moduli	ELSV formula Gromov–Witten invariant Hodge bundle Moduli of algebraic curves Stable curve

Morphisms	Hasse–Witt matrix Riemann–Hurwitz formula Prym variety Weber's theorem

Singularities	Acnode Crunode Cusp Delta invariant Tacnode

Vector bundles	Birkhoff–Grothendieck theorem Stable vector bundle Vector bundles on algebraic curves