Clement W. H. Lam

Clement Wing Hong Lam (Chinese: 林永康) is a Canadian mathematician, specializing in combinatorics. He is famous for the computer proof, with Larry Thiel and S. Swiercz, of the nonexistence of a finite projective plane of order 10.[1]

Lam earned his PhD in 1974 under Herbert Ryser at Caltech with thesis Rational G-Circulants Satisfying the Matrix Equation 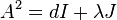A^2=d I+\lambda J.[2] He is a professor at Concordia University in Montreal.

In 2006 he received the Euler medal. In 1992 he received the Lester Randolph Ford Award for the article The search for a finite projective plane of order 10.[3] The eponymous Lam's problem is equivalent to finding a finite projective plane of order 10 or finding 9 orthogonal Latin squares of order 10.[4]

See also

References

  1. ↑ Clement W. H. Lam, Larry Thiel, S. Swiercz (1989). "The Nonexistence of Finite Projective Planes of Order 10". Canad. J. Math. 41: 1117–1123. doi:10.4153/cjm-1989-049-4.
  2. ↑ Clement W. H. Lam at the Mathematics Genealogy Project
  3. ↑ "The search for a finite projective plane of order 10". Amer. Math. Monthly 98: 305–318. 1991. doi:10.2307/2323798.
  4. ↑ Lam´s Problem at Mathworld

External links