Classical and quantum conductivity
Classical and quantum mechanical views of conductivity have both described the movements of electrons in a metallic solid. The free electron gas that is present in metallic solids is the reason for an important property of all metals: conductivity. This article will discuss the theory of conduction, specifically the theory of classical conduction whose defects were explained by the quantum theory. The modifications that the quantum theory adds to classical conduction not only explains the flaws that arose in the classical theory, but also adds a new dimension to conduction that is currently leading to new developments in the physics world.
Background
Solid states
With the advent of quantum mechanics, a greater understanding of the physical properties of solids was achieved. Solids can be split into two groups: amorphous and crystalline. Amorphous solid structures occur when a liquid is cooled too rapidly for the crystalline structure to form. Glass is a typical amorphous solid. When, however, ample time is allowed during the cooling of a liquid, then a crystalline structure will form. Within the category of crystalline structures, several different types of bonding are possible. These include ionic bonding, covalent bonding, and metallic bonding. The structure of a specific crystal is dependent on the bonding type, along with the sizes of the atoms involved.
Ionic crystals can form in as many as fourteen different shapes. The face-centered cubic structure is a common shape where the crystal’s smallest unit, the unit cell, is a cube, with the smaller of the two ions occupying the center of each face of the cube. In the body-centered cubic structure, eight of the larger ions form a cubic shape, while one of the smaller ions occupies its center. A hexagonal close-packed crystal structure is obtained by stacking identical spheres, and fitting these stacks into the triangular depressions of adjacent stacks.
Electrostatic energy
The net attractive portion of the potential energy of an ion in a crystal is dependent on the following: the square of the electric charge of an electron, the Boltzmann constant, the inverse of the distance between ions, as well as the Madelung constant. The Madelung constant is the result of a mathematical sum, which is dependent on the number of ions at a certain distance from a given ion. The repelling portion of the potential energy of an ion is dependent on a constant A, and inversely, exponentially dependent on the distance between ions. By writing an equation for the total potential energy (the sum of the attractive and repulsive portions), taking its derivative with respect to the distance between ions (which is equal to the force at equilibrium separation), as well as setting that result equal to zero and using the equilibrium separation as the distance between ions, then the constant, A, can be determined. Using all of this information, a simple expression can be written for the total potential energy of the ion. Now it is dependent only on the Madelung constant, Boltzmann’s constant, the equilibrium separation, the square of the charge of an electron, and a number n (the exponential factor for the distance between ions in the repulsive portion of the potential energy). Since the equilibrium separation can be determined experimentally, and the total potential energy can be accurately estimated based on the lattice energy of the ionic crystal, this number, n, can be determined as well.
The structure of covalently bonded crystals is determined by the directional nature of the bonds. This directional nature is a result of the specific hybridizations that exist for different shapes.
Quantum mechanics
Along with bonding type and atomic radii, metallic crystalline structures are also dependent on a quantum-mechanical mechanism. Unlike other crystals, in a metallically bonded solid, the electrons move freely throughout the solid, which are held in the solid by their attraction to the positively charged nuclei. A Schrödinger equation is used to display the wave function of electrons, which is dependent on the quantum numbers n and l, along with a constant, the Bohr radius, and the distance of the electrons from an ion core. It can also be shown from the probability density of an electron, that the electrons in a metallic solid are generally closer to the ionic cores than they were as individual atoms. This causes a decrease in the potential energy of the electrons. However, the assembly of the solid structure also confines the electrons to a smaller space than that in which they normally operate. This results in an increase in the kinetic energy of the electrons. The stability of the structure is a result of the fact that the decrease in potential energy is much more drastic than the increase in kinetic energy. The larger the atomic radius of an atom, the greater the decrease in potential energy will be when the metal solid is formed. Also, the fewer valence electrons an atom has, the smaller the increase in kinetic energy will be. Together these trends explain the observation that elements to the left and lower down the periodic table are more likely to be metals.
Conductivity
Classical conductivity
Around 1900, Paul Drude developed the foundation for classical conduction. He reasoned that since metals conduct electricity so well, they must contain free electrons that move through a lattice of positive ions. This motion of electrons led to the formation of Ohm's laws, as well as related the motion in a conductor to two types of conduction: heat and electrical. The free-moving electrons act just as a gas would; moving in every direction throughout the lattice. These electrons collide with the lattice ions as they move about, which is key in understanding thermal equilibrium. The average velocity due to the thermal energy is zero since the electrons are going in every direction, leading to velocity vectors that are randomly oriented. What is not zero, and is in fact a high value, is the speed of these electrons, which can be calculated using the equation
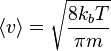
There is a way of affecting this free motion of electrons, which is by use of an electric field. This process is known as electrical conduction. An electric field provides a potential difference along a wire of electrons, which creates a force, 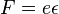 , where
, where  is the charge of an electron and
is the charge of an electron and  is the magnitude of the electric field. That force accelerates the electrons, as expected by Newton’s second law. The electrons are given a velocity away from the (negative source of the) field, which leads to these collisions with the fixed ions. The collisions rid the electrons of their kinetic energy momentarily, transferring that energy to the ion lattice in the form of heat, until the field again provides this sort of "push" to the electrons. The net result of all of this pushing and stopping (or gaining of kinetic energy and then a release of it), is a small value called drift velocity. To better understand this concept, one could picture a busload of kids (electrons), who are energetically moving about on the bus (wire). The kids have instantaneous velocities, but after colliding with each other and bouncing back to their seats the average velocity of the kids is zero. However, as the bus moves forward, the kids have a small drift velocity in the direction of the motion of the bus. The drift that is opposite of the electric field is in fact an electric current.
is the magnitude of the electric field. That force accelerates the electrons, as expected by Newton’s second law. The electrons are given a velocity away from the (negative source of the) field, which leads to these collisions with the fixed ions. The collisions rid the electrons of their kinetic energy momentarily, transferring that energy to the ion lattice in the form of heat, until the field again provides this sort of "push" to the electrons. The net result of all of this pushing and stopping (or gaining of kinetic energy and then a release of it), is a small value called drift velocity. To better understand this concept, one could picture a busload of kids (electrons), who are energetically moving about on the bus (wire). The kids have instantaneous velocities, but after colliding with each other and bouncing back to their seats the average velocity of the kids is zero. However, as the bus moves forward, the kids have a small drift velocity in the direction of the motion of the bus. The drift that is opposite of the electric field is in fact an electric current.
The electric current (amount of charge through a cross sectional area per unit time) is proportional to the voltage drop across two points, which is called Ohm’s Law and is given by 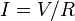 . The relationship of the current to the drift velocity as discussed above is given by
. The relationship of the current to the drift velocity as discussed above is given by 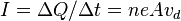 , where
, where  is the cross sectional area,
is the cross sectional area, 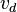 is the drift velocity,
is the drift velocity,  is the electron charge, and
is the electron charge, and  is the number of electrons per unit volume. The reason that this equation is significant is because Ohm’s law can be written as
is the number of electrons per unit volume. The reason that this equation is significant is because Ohm’s law can be written as 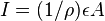 , (or
, (or 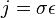 ) as well as in terms of the drift velocity
) as well as in terms of the drift velocity 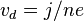 . The drift velocity is much smaller than the average thermal speed of the electrons, and so the electric field has no effect on the
. The drift velocity is much smaller than the average thermal speed of the electrons, and so the electric field has no effect on the 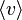 of the electrons. Ohm’s law says that the resistivity
of the electrons. Ohm’s law says that the resistivity  and conductivity
and conductivity  must be independent of
must be independent of  . This is important to the classical theory because it shows that according to Ohm’s law, since
. This is important to the classical theory because it shows that according to Ohm’s law, since 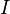 is proportional to
is proportional to  , there is a steady state situation where drift velocity is proportional to the field
, there is a steady state situation where drift velocity is proportional to the field  .
.
The entire "objective" of the classical theory is to explain resistivity in terms of the above-discussed properties of metals. By using the classical theory, one should be able to decide which metal to use for a certain purpose and be able to differentiate between different metals by use of these properties.
The journey of an electron can be expressed in another way, which is by use of the mean free path. The mean free path λ is the average distance traveled by electrons before their collisions. An electron moves through the lattice ions of a metal, and when the electron approaches the center of an ion, there is a collision at a distance r from the center. Once it collides with an ion, the electron is now hurdled in another direction until it collides with another ion. This zigzagging formation enables the electron to have a number of collisions in time t given by naπr2vt. This distance between collisions is related to the speed and time before collisions by use of the equation λ = <v>τ. At this point we assume the resistivity is given by ρ = (me<v>)/(ne2λ). Notice how there is no dependence on ε, since the mean free path depends only on the size and density of the ions. The abovementioned drift velocity can be expressed in terms of the mean free path as Vd = eλε/me<v>. One last expression, is that the mean free path is expressed by λ = (vt/naπr²vt) =1/naπr², where it is extremely important to emphasize here that the r here is the radius of those lattice ions that the electrons bounce off of.
Flaws in classical conductivity
While the classical understanding of conduction is useful in constructing Ohm’s law and providing an understanding of the motion of electrons, there are a number of inherent flaws in this theory. Firstly, the above stated equation for resistivity will give a value that is about seven times the measured value of resistivity at a temperature of 300 K. Furthermore, it can be shown by experiment that resistivity has a linear relationship with temperature, while the resistivity in accordance to the classical theory is reliant on the value <v>, which is related to the square root of temperature. There are some flaws from a statistical perspective as well. Applying Boltzmann statistics and the Maxwell distribution of speeds, the electrons that are viewed as particles will give an average kinetic energy of (3/2)kT. The molar heat capacity of a metal is expected to be (3/2)R greater than that of insulators, which has a heat capacity of 3R. In other words, it is expected that the molar heat capacity of metals will be (9/2)R. However, this is not observed. The experimentally determined molar heat capacity of metals is close to 3R. One last problem, (which will actually be key in the quantum solutions) is that it is known that electrons share wave-like properties as well, and the classical theory makes no mention of such properties.
Quantum conductivity
Before explaining how the quantum theory solves these flaws, there are a number of concepts that need to be understood. The first concept is that of the uncertainty principle, which states that since it is already known that the electrons are present in the space of the metal (i.e., something about its position is known), then there can not be zero kinetic energy (it must have some speed). This is very different from the classical viewpoint where it is assumed that at T=0 all the electrons would have a kinetic energy of zero. Also, the exclusion principle prevents more than two electrons from being present in the lowest energy level. This means that there are two electrons in each energy level.
By applying these concepts and creating a new quantum understanding of conduction, the problems that existed with the classical theory now disappear. In the classical theory it was shown that the square root of <v> was proportional to the resistivity. Now, since the net shift of velocity of all the electrons in an electric field is really the same as shifting only the Fermi electrons, in the case of thermal conductivity, the Fermi velocity can replace the <v> in the classical equation for resistivity. Then, since there is no temperature dependency involved in the Fermi speed, there no longer exists the problem of conflicting experimental and theoretical relationships between speed and temperature.
There is one important change that must be made to ensure the validity of these equations, and that is in regard to the collisions of electrons. In the classical theory, the collision was seen as similar to that of a ball with a wall: a particle bouncing off another. In the quantum understanding, an electron is viewed as a wave traveling through a medium. When the wavelength of the electrons is larger than the crystal spacing, the electrons will propagate freely throughout the metal without collision, therefore their scattering is only the result of imperfections in the crystal lattice of the metal. These imperfections are the results of such changes as thermal vibrations. This means that the ion’s cross sectional area is no longer important, but rather the amplitude of these vibrations and the deviations of these ions are what determines the mean free path. Fittingly, the r that was emphasized in the classical mean free path equation as being the radius of the ions, is now replaced with an r representing the amplitude of the oscillation of those ions. The beauty of this change is that now the mean free path equation gives a linearly proportional relationship between ρ and T, and not the problematic T.05 relationship.