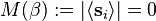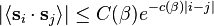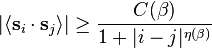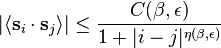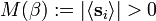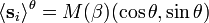Classical XY model
The classical XY model (sometimes also called classical rotor (rotator) model or O(2) model) is a lattice model of statistical mechanics. It is the special case of the n-vector model for n = 2.
Definition
Given a D-dimensional lattice Λ, per each lattice site j ∈ Λ there is a two-dimensional, unit-length vector sj = (cos θj, sin θj)
The spin configuration, s = (sj)j ∈ Λ is an assignment of the angle −π < θj ≤ π for each j ∈ Λ.
Given a translation-invariant interaction Jij = J(i − j) and a point dependent external field 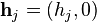 , the configuration energy is
, the configuration energy is
The case in which Jij = 0 except for ij nearest neighbor is called nearest neighbor case.
The configuration probability is given by the Boltzmann distribution with inverse temperature β ≥ 0:
where Z is the normalization, or partition function.[1] The notation 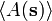 indicates the expectation of the random variable A(s) in the infinite volume limit, after periodic boundary conditions have been imposed.
indicates the expectation of the random variable A(s) in the infinite volume limit, after periodic boundary conditions have been imposed.
General properties
- The existence of the thermodynamic limit for the free energy and spin correlations were proved by Ginibre, extending to this case the Griffiths inequality.[2]
- Using the Griffiths inequality in the formulation of Ginibre, Aizenman and Simon[3] proved that the two point spin correlation of the ferromagnetics XY model in dimension D, coupling J > 0 and inverse temperature β is dominated by (i.e. has an upper bound given by) the two point correlation of the ferromagnetic Ising model in dimension D, coupling J > 0 and inverse temperature β/2
- Hence the critical β of the XY model cannot be smaller than the double of the critical temperature of the Ising model
One dimension
- In case of long range interaction,
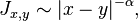 the thermodynamic limit is well defined if α > 1; the magnetization remains zero if α ≥ 2; but the magnetization is positive, at low enough temperature, if 1 < α < 2 (infrared bounds).
the thermodynamic limit is well defined if α > 1; the magnetization remains zero if α ≥ 2; but the magnetization is positive, at low enough temperature, if 1 < α < 2 (infrared bounds).
- As in any 'nearest-neighbor' n-vector model with free boundary conditions, if the external field is zero, there exists a simple exact solution. In the free boundary conditions case, the Hamiltonian is
- therefore the partition function factorizes under the change of coordinates
- That gives
- Finally
- where
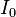 is the modified Bessel function of the first kind.
is the modified Bessel function of the first kind.
- The same computation for periodic boundary condition (and still h = 0) requires the transfer matrix formalism.[4]
Two Dimensions
- In the case of long range interaction,
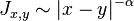 , the thermodynamic limit is well defined if α > 2; the magnetization remains zero if α ≥ 4; but the magnetization is positive at low enough temperature if 2 < α < 4 (Kunz and Pfister; alternatively, infrared bounds).
, the thermodynamic limit is well defined if α > 2; the magnetization remains zero if α ≥ 4; but the magnetization is positive at low enough temperature if 2 < α < 4 (Kunz and Pfister; alternatively, infrared bounds).
- At high temperature and nearest neighbour interaction, the spontaneous magnetization vanishes:
- Besides, cluster expansion shows that the spin correlations cluster exponentially fast: for instance
- At low temperature and nearest neighbour interaction, i.e. β ≫ 1, the spontaneous magnetization remains zero, (Mermin theorem)
- but the decay of the correlations is only power law: Fröhlich and Spencer[5] found the lower bound
- while McBryan and Spencer found the upper bound, for any
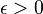
The fact that at high temperature correlations decay exponentially fast, while at low temperatures decay with power law, even though in both regimes M(β) = 0, is called Kosterlitz-Thouless transition.
The continuous version of the XY model is often used to model systems that possess order parameters with the same kinds of symmetry, e.g. superfluid helium, hexatic liquid crystals. This is what makes them peculiar from other phase transitions which are always accompanied with a symmetry breaking. Topological defects in the XY model leads to a vortex-unbinding transition from the low-temperature phase to the high-temperature disordered phase.
Three and Higher Dimensions
Independently of the range of the interaction, at low enough temperature the magnetization is positive.
- At high temperature, the spontaneous magnetization vanishes:
- Besides, cluster expansion shows that the spin correlations cluster exponentially fast: for instance
- At low temperature, infrared bound shows that the spontaneous magnetization is strictly positive:
- Besides, there exist a 1-parameter family of extremal states,
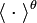 , such that
, such that
- but, conjecturally, in each of these extremal states the truncated correlations decay algebraically.
In general, the XY model can be seen as a specialization of Stanley's N-vector model [6]
See also
- Classical Heisenberg model
- Goldstone boson
- Ising model
- Potts model
- N-vector model
- Kosterlitz-Thouless transition
- Topological defect
- Superfluid film
References
- ↑ Lubensky, Chaikin (2000). Principles of Condensed Matter Physics. Cambridge University Press. p. 699. ISBN 0-521-79450-1.
- ↑ Ginibre, J. (1970). "General formulation of Griffiths' inequalities". Comm. Math. Phys. 16 (4): 310–328. Bibcode:1970CMaPh..16..310G. doi:10.1007/BF01646537.
- ↑ Aizenman, M.; Simon, B. (1980). "A comparison of plane rotor and Ising models". Phys. Lett. A 76. Bibcode:1980PhLA...76..281A. doi:10.1016/0375-9601(80)90493-4.
- ↑ Mattis, D.C. (1984). "Transfer matrix in plane-rotator model". Phys. Lett. 104 A. Bibcode:1984PhLA..104..357M. doi:10.1016/0375-9601(84)90816-8.
- ↑ Fröhlich, J.; Spencer, T. (1981). "The Kosterlitz–Thouless transition in two-dimensional abelian spin systems and the Coulomb gas". Comm. Math. Phys. 81 (4): 527–602. doi:10.1007/bf01208273.
- ↑ Stanley, H.E. "Dependence of Critical Properties on Dimensionality of Spins". Phys. Rev. Lett. 20: 589. Bibcode:1968PhRvL..20..589S. doi:10.1103/PhysRevLett.20.589.
- Evgeny Demidov, Vortices in the XY model (2004)
General Literature
- H. E. Stanley, Introduction to Phase Transitions and Critical Phenomena, (Oxford University Press, Oxford and New York 1971);
- H. Kleinert, Gauge Fields in Condensed Matter, Vol. I, " SUPERFLOW AND VORTEX LINES", pp. 1–742, Vol. II, "STRESSES AND DEFECTS", pp. 743–1456, World Scientific (Singapore, 1989); Paperback ISBN 9971-5-0210-0 (also available online: Vol. I and Vol. II)
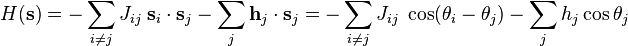
![P(\mathbf{s})=\frac{e^{-\beta H(\mathbf{s})}}{Z} \qquad Z=\int_{[-\pi,\pi]^{\Lambda}} \prod_{j\in \Lambda}d\theta_j\;e^{-\beta H(\mathbf{s})}.](../I/m/4441bd84d97af9cdb649f166836fc53e.png)
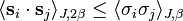
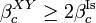
![H(\mathbf{s}) = - J [\cos(\theta_1-\theta_2)+\cdots+\cos(\theta_{L-1}-\theta_L)]](../I/m/19aa7d08602594716d3c67261d26d188.png)
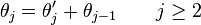
![Z=\int_{-\pi}^{\pi}d\theta_1\cdots d\theta_L\; e^{\beta J\cos(\theta_1-\theta_2)}\cdots e^{\beta J\cos(\theta_{L-1}-\theta_L)}=2\pi \prod_{j=2}^L\int_{-\pi}^{\pi}d\theta'_j\;e^{\beta J\cos\theta'_j}=2\pi\left[\int_{-\pi}^{\pi}d\theta'_j\;e^{\beta J\cos\theta'_j}\right]^{L-1}](../I/m/6968c4a9c4bf23c175e7803686142c0a.png)
![f(\beta, 0)=-\frac{1}{\beta}\ln \int_{-\pi}^{\pi}d\theta'_j\;e^{\beta J \cos\theta'_j}=-\frac{1}{\beta}\ln [2\pi I_0(\beta J)]](../I/m/0a78de62a48956a008bef6bb4b7d62bd.png)