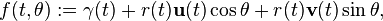Circular surface
In mathematics and, in particular, differential geometry a circular surface is the image of a map ƒ : I × S1 → R3, where I ⊂ R is an open interval and S1 is the unit circle, defined by
where γ, u, v : I → R3 and r : I → R>0, when R>0 := { x ∈ R : x > 0 }. Moreover, it is usually assumed that u · u = v · v = 1 and u · v = 0, where dot denotes the canonical scalar product on R3, i.e. u and v are unit length and mutually perpendicular. The map γ : I → R3 is called the base curve for the circular surface and the two maps u, v : I → R3 are called the direction frame for the circular surface. For a fixed t0 ∈ I the image of ƒ(t0, θ) is called a generating circle of the circular surface.[1]
Circular surfaces are an analogue of ruled surfaces. In the case of circular surfaces the generators are circles; called the generating circles. In the case of ruled surface the generators are straight lines; called rulings.
References
- ↑ S. Izumiya, K. Saji, and N. Takeuchi, "Circular Surfaces", Advances in Geometry, de Gruyter, Vol 7, 2007, 295–313.