Circuit rank
In graph-theoretic mathematics, the circuit rank, cyclomatic number, or nullity of an undirected graph  is the minimum number
is the minimum number  of edges to remove from
of edges to remove from  to remove all its cycles, making it into a forest. Unlike the corresponding feedback arc set problem for directed graphs, it is easily computed, using the simple formula
to remove all its cycles, making it into a forest. Unlike the corresponding feedback arc set problem for directed graphs, it is easily computed, using the simple formula
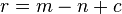 ,
,
where  is the number of edges in
is the number of edges in  ,
,  is the number of vertices, and
is the number of vertices, and  is the number of connected components.[1]
is the number of connected components.[1]
Under the name of cyclomatic number, the concept was introduced by Gustav Kirchhoff.[2][3]
Related concepts
The circuit rank is the corank of the graphic matroid of  ,[4] from which it can be seen that a greedy algorithm that removes edges one by one, at each step removing an edge that belongs to at least one cycle of the remaining graph, will necessarily find a set of
,[4] from which it can be seen that a greedy algorithm that removes edges one by one, at each step removing an edge that belongs to at least one cycle of the remaining graph, will necessarily find a set of  edges the removal of which leaves
edges the removal of which leaves  acyclic. Alternatively, such a set may be found as the complement of a spanning forest of
acyclic. Alternatively, such a set may be found as the complement of a spanning forest of  .
.
The cyclomatic number is also the dimension of the cycle space of  .[1] Topologically,
.[1] Topologically,  may be viewed as an example of a 1-dimensional simplicial complex, and its cyclomatic number is the rank of the first (integer) homology group of this complex,[5]
may be viewed as an example of a 1-dimensional simplicial complex, and its cyclomatic number is the rank of the first (integer) homology group of this complex,[5]
![r = \operatorname{rank}\left[H_1(G,\Z)\right]](../I/m/a3934a37f649a5a78245c97814f850ac.png) ,
,
and because of this the cyclomatic number is also called the first Betti number.[6] A variant of the circuit rank for planar graphs, normalized by dividing by the maximum possible circuit rank of any planar graph with the same vertex set, is called the meshedness coefficient.[7]
The circuit rank controls the number of ears in an ear decomposition of a graph: in a biconnected graph with circuit rank  , every open ear decomposition has exactly
, every open ear decomposition has exactly  ears.[8]
ears.[8]
Other numbers defined in terms of edge deletion from undirected graphs include the edge connectivity, the minimum number of edges to delete in order to disconnect the graph, and matching preclusion, the minimum number of edges to delete in order to prevent the existence of a perfect matching.
Almost trees
A graph with cyclomatic number  is also called a r-almost-tree, because only r edges need to be removed from the graph to make it into a tree or forest. A 1-almost-tree is a near-tree: a connected near-tree is a pseudotree, a cycle with a (possibly trivial) tree rooted at each vertex.[9]
is also called a r-almost-tree, because only r edges need to be removed from the graph to make it into a tree or forest. A 1-almost-tree is a near-tree: a connected near-tree is a pseudotree, a cycle with a (possibly trivial) tree rooted at each vertex.[9]
Several authors have studied the parameterized complexity of graph algorithms on r-near-trees, parameterized by  .[10][11]
.[10][11]
See also
- Cycle rank
- cyclomatic complexity is a straightforward application to the control flow graph used in software engineering
References
- ↑ 1.0 1.1 Berge, Claude (2001), "Cyclomatic number", The Theory of Graphs, Courier Dover Publications, pp. 27–30, ISBN 9780486419756.
- ↑ Peter Robert Kotiuga (2010). A Celebration of the Mathematical Legacy of Raoul Bott. American Mathematical Soc. p. 20. ISBN 978-0-8218-8381-5.
- ↑ Per Hage (1996). Island Networks: Communication, Kinship, and Classification Structures in Oceania. Cambridge University Press. p. 48. ISBN 978-0-521-55232-5.
- ↑ Berge, Claude (1976), Graphs and Hypergraphs, North-Holland Mathematical Library 6, Elsevier, p. 477, ISBN 9780720424539.
- ↑ Serre, Jean-Pierre (2003), Trees, Springer Monographs in Mathematics, Springer, p. 23.
- ↑ Gregory Berkolaiko; Peter Kuchment (2013). Introduction to Quantum Graphs. American Mathematical Soc. p. 4. ISBN 978-0-8218-9211-4.
- ↑ Buhl, J.; Gautrais, J.; Sole, R.V.; Kuntz, P.; Valverde, S.; Deneubourg, J.L.; Theraulaz, G. (2004), "Efficiency and robustness in ant networks of galleries", The European Physical Journal B-Condensed Matter and Complex Systems (Springer-Verlag) 42 (1): 123–129, doi:10.1140/epjb/e2004-00364-9.
- ↑ Whitney, H. (1932), "Non-separable and planar graphs", Transactions of the American Mathematical Society 34: 339–362, doi:10.2307/1989545. See in particular Theorems 18 (relating ear decomposition to circuit rank) and 19 (on the existence of ear decompositions).
- ↑ Brualdi, Richard A. (2006), Combinatorial matrix classes, Encyclopedia of Mathematics and Its Applications 108, Cambridge: Cambridge University Press, p. 349, ISBN 0-521-86565-4, Zbl 1106.05001
- ↑ Coppersmith, Don; Vishkin, Uzi (1985), "Solving NP-hard problems in 'almost trees': Vertex cover", Discrete Applied Mathematics 10 (1): 27–45, doi:10.1016/0166-218X(85)90057-5, Zbl 0573.68017.
- ↑ Fiala, Jiří; Kloks, Ton; Kratochvíl, Jan (2001), "Fixed-parameter complexity of λ-labelings", Discrete Applied Mathematics 113 (1): 59–72, doi:10.1016/S0166-218X(00)00387-5, Zbl 0982.05085.