Circle packing in an isosceles right triangle
Circle packing in a right isosceles triangle is a packing problem where the objective is to pack n unit circles into the smallest possible isosceles right triangle.
Minimum solutions (lengths shown are length of leg) are shown in the table below.[1] Solutions to the equivalent problem of maximizing the minimum distance between n points in an isosceles right triangle, are known to be optimal for n< 8.[2] In 2011 a heuristic algorithm found 18 improvements on previously known optima, the smallest of which was for n=13.[3]
| Number of circles |
Length |
| 1 |
3.414... |
| 2 |
4.828... |
| 3 |
5.414... |
| 4 |
6.242... |
| 5 |
7.146... |
| 6 |
7.414... 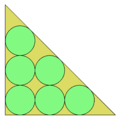 |
| 7 |
8.181... |
| 8 |
8.692... |
| 9 |
9.071... |
| 10 |
9.414... |
| 11 |
10.059... |
| 12 |
10.422... |
| 13 |
10.798... |
| 14 |
11.141... |
| 15 |
11.414... |
References
- ↑ Specht, Eckard (2011-03-11). "The best known packings of equal circles in an isosceles right triangle". Retrieved 2011-05-01.
- ↑ Xu, Y. (1996). "On the minimum distance determined by n (≤ 7) points in an isoscele right triangle". Acta Mathematicae Applicatae Sinica 12 (2): 169–175. doi:10.1007/BF02007736.
- ↑ López, C. O.; Beasley, J. E. (2011). "A heuristic for the circle packing problem with a variety of containers". European Journal of Operational Research 214 (3): 512. doi:10.1016/j.ejor.2011.04.024.
