Chronology of computation of π
The table below is a brief chronology of computed numerical values of, or bounds on, the mathematical constant pi (π). For more detailed explanations for some of these calculations, see Approximations of π.
| Date | Who | Value of pi (world records in bold) |
|---|---|---|
| 26th century BC | Egyptian Great Pyramid of Giza and Meidum Pyramid[1] | 3+1/7 = 22/7 = 3.142... |
| 434 BC | Anaxagoras attempted to square the circle with compass and straightedge | |
| c. 250 BC | Archimedes | 223/71 < π < 22/7 (3.140845... < π < 3.142857...) |
| 20 BC | Vitruvius | 25/8 = 3.125 |
| 5 | Liu Xin | 3.1457 |
| 130 | Zhang Heng | √10 = 3.162277... 730/232 = 3.146551... |
| 150 | Ptolemy | 377/120 = 3.141666... |
| 250 | Wang Fan | 142/45 = 3.155555... |
| 263 | Liu Hui | 3.141024 < π < 3.142074 3927/1250 = 3.1416 |
| 400 | He Chengtian | 111035/35329 = 3.142885... |
| 480 | Zu Chongzhi | 3.1415926 < π < 3.1415927 Zu's ratio 355/113 = 3.1415929 |
| 499 | Aryabhata | 62832/20000 = 3.1416 |
| 640 | Brahmagupta | √10 = 3.162277... |
| 800 | Al Khwarizmi | 3.1416 |
| 1150 | Bhāskara II | 3.14156 |
| 1220 | Fibonacci | 3.141818 |
| 1320 | Zhao Youqin | 3.141592+ |
| All records from 1400 onwards are given as the number of correct decimal places. | ||
| 1400 | Madhava of Sangamagrama probably discovered the infinite power series expansion of π, now known as the Leibniz formula for pi[2] | 10 decimal places |
| 1424 | Jamshīd al-Kāshī[3] | 17 decimal places |
| 1573 | Valentinus Otho (355/113) | 6 decimal places |
| 1579 | François Viète[4] | 9 decimal places |
| 1593 | Adriaan van Roomen[5] | 15 decimal places |
| 1596 | Ludolph van Ceulen | 20 decimal places |
| 1615 | 32 decimal places | |
| 1621 | Willebrord Snell (Snellius), a pupil of Van Ceulen | 35 decimal places |
| 1630 | Christoph Grienberger[6][7] | 38 decimal places |
| 1665 | Isaac Newton | 16 decimal places |
| 1681 | Takakazu Seki[8] | 11 decimal places 16 decimal places |
| 1699 | Abraham Sharp calculated pi to 72 digits, but not all were correct | 71 decimal places |
| 1706 | John Machin | 100 decimal places |
| 1706 | William Jones introduced the Greek letter 'π' | |
| 1719 | Thomas Fantet de Lagny calculated 127 decimal places, but not all were correct | 112 decimal places |
| 1722 | Toshikiyo Kamata | 24 decimal places |
| 1722 | Katahiro Takebe | 41 decimal places |
| 1739 | Yoshisuke Matsunaga | 51 decimal places |
| 1748 | Leonhard Euler used the Greek letter 'π' in his book Introductio in Analysin Infinitorum and assured its popularity. | |
| 1761 | Johann Heinrich Lambert proved that π is irrational | |
| 1775 | Euler pointed out the possibility that π might be transcendental | |
| 1789 | Jurij Vega calculated 143 decimal places, but not all were correct | 126 decimal places |
| 1794 | Jurij Vega calculated 140 decimal places, but not all were correct | 136 decimal places |
| 1794 | Adrien-Marie Legendre showed that π² (and hence π) is irrational, and mentioned the possibility that π might be transcendental. | |
| Late 18th century | Anonymous manuscript turns up at Radcliffe Library, in Oxford, England, discovered by F. X. von Zach, giving the value of pi to 154 digits, 152 of which were correct | 152 decimal places |
| 1841 | William Rutherford calculated 208 decimal places, but not all were correct | 152 decimal places |
| 1844 | Zacharias Dase and Strassnitzky calculated 205 decimal places, but not all were correct | 200 decimal places |
| 1847 | Thomas Clausen calculated 250 decimal places, but not all were correct | 248 decimal places |
| 1853 | Lehmann | 261 decimal places |
| 1855 | Richter | 500 decimal places |
| 1874 | William Shanks took 15 years to calculate 707 decimal places but not all were correct (the error was found by D. F. Ferguson in 1946) | 527 decimal places |
| 1882 | Ferdinand von Lindemann proved that π is transcendental (the Lindemann–Weierstrass theorem) | |
| 1897 | The U.S. state of Indiana came close to legislating the value of 3.2 (among others) for π. House Bill No. 246 passed unanimously. The bill stalled in the state Senate due to a suggestion of possible commercial motives involving publication of a textbook.[9] | |
| 1910 | Srinivasa Ramanujan found several rapidly converging infinite series of π, which can compute 8 decimal places of π with each term in the series. Since the 1980s, his series have become the basis for the fastest algorithms currently used by Yasumasa Kanada and the Chudnovsky brothers to compute π. | |
| 1946 | D. F. Ferguson (using a desk calculator) | 620 decimal places |
| 1947 | Ivan Niven gave a very elementary proof that π is irrational | |
| January 1947 | D. F. Ferguson (using a desk calculator) | 710 decimal places |
| September 1947 | D. F. Ferguson (using a desk calculator) | 808 decimal places |
| 1949 | D. F. Ferguson and John Wrench, using a desk calculator | 1,120 decimal places |
| All records from 1949 onwards were calculated with electronic computers. | ||
| 1949 | John Wrench, and L. R. Smith were the first to use an electronic computer (the ENIAC) to calculate π (it took 70 hours) (also attributed to Reitwiesner et al.) [10] | 2,037 decimal places |
| 1953 | Kurt Mahler showed that π is not a Liouville number | |
| 1954 | S. C. Nicholson & J. Jeenel, using the NORC (13 minutes) [11] | 3,093 decimal places |
| 1957 | George E. Felton, using the Ferranti Pegasus computer (London), calculated 10,021 digits, but not all were correct [12] | 7,480 decimal places |
| January 1958 | Francois Genuys, using an IBM 704 (1.7 hours) [13] | 10,000 decimal places |
| May 1958 | George E. Felton, using the Pegasus computer (London) (33 hours) | 10,021 decimal places |
| 1959 | Francois Genuys, using the IBM 704 (Paris) (4.3 hours) [14] | 16,167 decimal places |
| 1961 | Daniel Shanks and John Wrench, using the IBM 7090 (New York) (8.7 hours) <ref name="Calculation of Pi to 100,000 Decimals" in the journal Mathematics of Computation, vol 16 (1962), issue 77, page 76-99."> "Calculation of Pi to 100,000 Decimals" in the journal Mathematics of Computation, vol 16 (1962), issue 77, pages 76–99.</ref> | 100,265 decimal places |
| 1961 | J.M. Gerard, using the IBM 7090 (London) (39 minutes) | 20,000 decimal places |
| 1966 | Jean Guilloud and J. Filliatre, using the IBM 7030 (Paris) (taking 28 hours??) | 250,000 decimal places |
| 1967 | Jean Guilloud and M. Dichampt, using the CDC 6600 (Paris) (28 hours) | 500,000 decimal places |
| 1973 | Jean Guilloud and Martin Bouyer, using the CDC 7600 (23.3 hours) | 1,001,250 decimal places |
| 1981 | Kazunori Miyoshi and Yasumasa Kanada, FACOM M-200 | 2,000,036 decimal places |
| 1981 | Jean Guilloud, Not known | 2,000,050 decimal places |
| 1982 | Yoshiaki Tamura, MELCOM 900II | 2,097,144 decimal places |
| 1982 | Yoshiaki Tamura and Yasumasa Kanada, HITAC M-280H (2.9 hours) | 4,194,288 decimal places |
| 1982 | Yoshiaki Tamura and Yasumasa Kanada, HITAC M-280H | 8,388,576 decimal places |
| 1983 | Yasumasa Kanada, Sayaka Yoshino and Yoshiaki Tamura, HITAC M-280H | 16,777,206 decimal places |
| October 1983 | Yasunori Ushiro and Yasumasa Kanada, HITAC S-810/20 | 10,013,395 decimal places |
| October 1985 | Bill Gosper, Symbolics 3670 | 17,526,200 decimal places |
| January 1986 | David H. Bailey, CRAY-2 | 29,360,111 decimal places |
| September 1986 | Yasumasa Kanada, Yoshiaki Tamura, HITAC S-810/20 | 33,554,414 decimal places |
| October 1986 | Yasumasa Kanada, Yoshiaki Tamura, HITAC S-810/20 | 67,108,839 decimal places |
| January 1987 | Yasumasa Kanada, Yoshiaki Tamura, Yoshinobu Kubo and others, NEC SX-2 | 134,214,700 decimal places |
| January 1988 | Yasumasa Kanada and Yoshiaki Tamura, HITAC S-820/80 | 201,326,551 decimal places |
| May 1989 | Gregory V. Chudnovsky & David V. Chudnovsky, CRAY-2 & IBM 3090/VF | 480,000,000 decimal places |
| June 1989 | Gregory V. Chudnovsky & David V. Chudnovsky, IBM 3090 | 535,339,270 decimal places |
| July 1989 | Yasumasa Kanada and Yoshiaki Tamura, HITAC S-820/80 | 536,870,898 decimal places |
| August 1989 | Gregory V. Chudnovsky & David V. Chudnovsky, IBM 3090 | 1,011,196,691 decimal places |
| 19 November 1989 | Yasumasa Kanada and Yoshiaki Tamura, HITAC S-820/80 | 1,073,740,799 decimal places |
| August 1991 | Gregory V. Chudnovsky & David V. Chudnovsky, Homemade parallel computer (details unknown, not verified) [15] | 2,260,000,000 decimal places |
| 18 May 1994 | Gregory V. Chudnovsky & David V. Chudnovsky, New homemade parallel computer (details unknown, not verified) | 4,044,000,000 decimal places |
| 26 June 1995 | Yasumasa Kanada and Daisuke Takahashi, HITAC S-3800/480 (dual CPU) [16] | 3,221,220,000 decimal places |
| 28 August 1995 | Yasumasa Kanada and Daisuke Takahashi, HITAC S-3800/480 (dual CPU) [17] | 4,294,960,000 decimal places |
| 11 October 1995 | Yasumasa Kanada and Daisuke Takahashi, HITAC S-3800/480 (dual CPU) [18] | 6,442,450,000 decimal places |
| 6 July 1997 | Yasumasa Kanada and Daisuke Takahashi, HITACHI SR2201 (1024 CPU) [19] | 51,539,600,000 decimal places |
| 5 April 1999 | Yasumasa Kanada and Daisuke Takahashi, HITACHI SR8000 (64 of 128 nodes) [20] | 68,719,470,000 decimal places |
| 20 September 1999 | Yasumasa Kanada and Daisuke Takahashi, HITACHI SR8000/MPP (128 nodes) [21] | 206,158,430,000 decimal places |
| 24 November 2002 | Yasumasa Kanada & 9 man team, HITACHI SR8000/MPP (64 nodes), 600 hours, Department of Information Science at the University of Tokyo in Tokyo, Japan [22] | 1,241,100,000,000 decimal places |
| 29 April 2009 | Daisuke Takahashi et al., T2K Open Supercomputer (640 nodes), single node speed is 147.2 gigaflops, 29.09 hours, computer memory is 13.5 terabytes, Gauss–Legendre algorithm, Center for Computational Sciences at the University of Tsukuba in Tsukuba, Japan[23] | 2,576,980,377,524 decimal places |
| All records from Dec 2009 onwards are calculated on home computers with commercially available parts. | ||
| 31 December 2009 | Fabrice Bellard
|
2,699,999,990,000 decimal places |
| 2 August 2010 | Shigeru Kondo[26]
|
5,000,000,000,000 decimal places |
| 17 October 2011 | Shigeru Kondo[29]
|
10,000,000,000,050 decimal places |
| 28 December 2013 | Shigeru Kondo[30]
|
12,100,000,000,050 decimal places |
| 8 October 2014 | "houkouonchi"[31]
|
13,300,000,000,000 decimal places |

Graph showing how the record precision of numerical approximations to pi measured in decimal places (depicted on a logarithmic scale), evolved in human history. The time before 1400 is compressed.
See also
| Part of a series of articles on the |
| mathematical constant π |
|---|
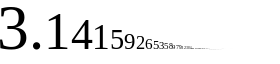 |
| Uses |
| Properties |
| Value |
| People |
| History |
| In culture |
| Related topics |
- History of pi
References
- ↑ Petrie, W.M.F. Surveys of the Great Pyramids. Nature Journal: 942–943. 1925
- ↑ Bag, A. K. (1980). "Indian Literature on Mathematics During 1400–1800 A.D." (PDF). Indian Journal of History of Science 15 (1): 86. — Madhava gave π ≈ 2,827,433,388,233/9×10−11 = 3.14159 26535 92222…, good to 10 decimal places.
- ↑ approximated 2π to 9 sexagesimal digits. Al-Kashi, author: Adolf P. Youschkevitch, chief editor: Boris A. Rosenfeld, p. 256 O'Connor, John J.; Robertson, Edmund F., "Ghiyath al-Din Jamshid Mas'ud al-Kashi", MacTutor History of Mathematics archive, University of St Andrews.. Azarian, Mohammad K. (2010), "al-Risāla al-muhītīyya: A Summary", Missouri Journal of Mathematical Sciences 22 (2): 64–85.
- ↑ Viète, François (1579). Canon mathematicus seu ad triangula : cum adpendicibus (in Latin).
- ↑ Romanus, Adrianus (1593). Ideae mathematicae pars prima, sive methodus polygonorum (in Latin).
- ↑ Grienbergerus, Christophorus (1630). Elementa Trigonometrica (PDF) (in Latin).
- ↑ Hobson, Ernest William (1913). "Squaring the Circle": a History of the Problem (PDF). p. 27.
- ↑ Yoshio, Mikami; Eugene Smith, David (April 2004) [January 1914]. A History of Japanese Mathematics (paperback ed.). Dover Publications. ISBN 0-486-43482-6.
- ↑ Lopez-Ortiz, Alex (February 20, 1998). "Indiana Bill sets value of Pi to 3". the news.answers WWW archive. Department of Information and Computing Sciences, Utrecht University. Retrieved 2009-02-01.
- ↑ G. Reitwiesner, "An ENIAC determination of Pi and e to more than 2000 decimal places," MTAC, v. 4, 1950, pp. 11–15"
- ↑ S. C, Nicholson & J. Jeenel, "Some comments on a NORC computation of x," MTAC, v. 9, 1955, pp. 162–164
- ↑ G. E. Felton, "Electronic computers and mathematicians," Abbreviated Proceedings of the Oxford Mathematical Conference for Schoolteachers and Industrialists at Trinity College, Oxford, April 8–18, 1957, pp. 12–17, footnote pp. 12–53. This published result is correct to only 7480D, as was established by Felton in a second calculation, using formula (5), completed in 1958 but apparently unpublished. For a detailed account of calculations of x see J. W. Wrench, Jr., "The evolution of extended decimal approximations to x," The Mathematics Teacher, v. 53, 1960, pp. 644–650
- ↑ F. Genuys, "Dix milles decimales de x," Chiffres, v. 1, 1958, pp. 17–22.
- ↑ This unpublished value of x to 16167D was computed on an IBM 704 system at the Commissariat à l'Energie Atomique in Paris, by means of the program of Genuys
- ↑ Bigger slices of Pi (determination of the numerical value of pi reaches 2.16 billion decimal digits) Science News 24 August 1991 http://www.encyclopedia.com/doc/1G1-11235156.html
- ↑ ftp://pi.super-computing.org/README.our_last_record_3b
- ↑ ftp://pi.super-computing.org/README.our_last_record_4b
- ↑ ftp://pi.super-computing.org/README.our_last_record_6b
- ↑ ftp://pi.super-computing.org/README.our_last_record_51b
- ↑ ftp://pi.super-computing.org/README.our_last_record_68b
- ↑ ftp://pi.super-computing.org/README.our_latest_record_206b
- ↑ http://www.super-computing.org/pi_current.html
- ↑ http://www.hpcs.is.tsukuba.ac.jp/~daisuke/pi.html
- ↑ http://bellard.org
- ↑ http://bellard.org/pi/pi2700e9/pipcrecord.pdf
- ↑ Shigeru Kondo
- ↑ y-cruncher – A Multi-Threaded Pi-Program
- ↑ Kondo's 2010 record, A. Yee's program y-cruncher
- ↑ Pi – 10 Trillion Digits
- ↑ Pi - 12.1 Trillion Digits
- ↑ Pi - 13.3 Trillion Digits
External links
- Borwein, Jonathan, "The Life of Pi"
- Kanada Laboratory home page
- Stu's Pi page
- Takahashi's page