Chromatographic response function
Chromatographic response function, often abbreviated to CRF, is a coefficient which measures the quality of the separation in the result of a chromatography.
The CRF concept have been created during the development of separation optimization, to compare the quality of many simulated or real chromatographic separations. Many CRFs have been proposed and discussed.
In high performance liquid chromatography the CRF is calculated from various parameters of the peaks of solutes (like width, retention time, symmetry etc.) are considered into the calculation. In TLC the CRFs are based on the placement of the spots, measured as RF values.
CRFs examples in thin layer chromatography
The CRFs in thin layer chromatography characterize the equal-spreading of the spots. The ideal case, when the RF of the spots are uniformly distributed in <0,1> range (for example 0.25,0.5 and 0.75 for three solutes) should be characterized as the best situation possible.
The simplest criteria are 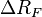 and
and 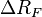 product (Wang et al., 1996). They are the smallest difference between sorted RF values, or product of such differences.
product (Wang et al., 1996). They are the smallest difference between sorted RF values, or product of such differences.
Another function is the multispot response function (MRF) as developed by De Spiegeleer et al. It is based also of differences product. This function always lies between 0 and 1. When two RF values are equal, it is equal to 0, when all RF values are equal-spread, it is equal to 1. The L and U values - upper and lower limit of RF - give possibility to avoid the band region.
![MRF = \frac {(U - hR_{Fn})(hR_{F1} - L)\prod^{n-1}_{i=1}(hR_{Fi+1} - hR_{Fi})} {[(U - L)/(n+1)]^{n+1}}](../I/m/6a772ca080e396f8a254af4e7050ffc1.png)
The last example of coefficient sensitive to minimal distance between spots is Retention distance (Komsta et al., 2007)
![R_D = \Bigg[(n+1)^{(n+1)} \prod^n_{i=0}{(R_{F(i+1)}-R_{Fi})\Bigg]^{\frac{1}{n}}}](../I/m/177edfe470852f4dfe1753312d3d8fb2.png)
The second group are criteria insensitive for minimal difference between RF values (if two compounds are not separated, such CRF functions will not indicate it). They are equal to zero in equal-spread state increase when situation is getting worse.
There are:
Separation response (Bayne et al., 1987)
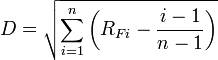
Performance index (Gocan et al., 1991)
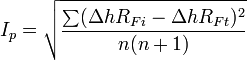
Informational entropy (Gocan et al., 1991, second reference)
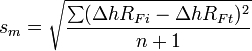
Retention uniformity (Komsta et al., 2007)
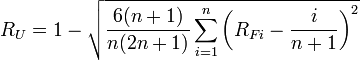
In all above formulas, n is the number of compounds separated, Rf (1...n) are the Retention factor of the compounds sorted in non-descending order, Rf0 = 0 and Rf(n+1) = 1.
References
- Q.S. Wang, B.W. Yan, J. Planar Chromatogr. 9 (1996) 192.
- B.J.M. de Spiegeleer, P.H.M. de Meloose, G.A.S. Seghers, Anal. Chem. 59 (1987) 62.
- C.K. Bayne, C.Y. Ma, J. Liq. Chromatogr. 10 (1987) 3529.
- S. Gocan, M. Mihaly, Stud Univ B-B Chemia, 1 (1991) 18.
- S. Gocan, J. Planar Chromatogr. 4 (1991) 169.
- Ł. Komsta, W. Markowski, G. Misztal, J. Planar Chromatogr. 20 (2007) 27.