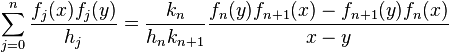Christoffel–Darboux formula

In mathematics, the Christoffel–Darboux theorem is an identity for a sequence of orthogonal polynomials, introduced by Elwin Bruno Christoffel (1858) and Jean Gaston Darboux (1878). It states that

\sum_{j=0}^n \frac{f_j(x) f_j(y)}{h_j} = \frac{k_n}{h_n k_{n+1}} \frac{f_n(y) f_{n+1}(x) - f_{n+1}(y) f_n(x)}{x - y}

where f_j(x) is the jth term of a set of orthogonal polynomials of squared norm h_j and leading coefficient k_j.

References

Andrews, George E.; Askey, Richard; Roy, Ranjan (1999), Special functions, Encyclopedia of Mathematics and its Applications 71, Cambridge University Press, ISBN 978-0-521-62321-6, MR 1688958
Christoffel, E. B. (1858), "Über die Gaußische Quadratur und eine Verallgemeinerung derselben.", Journal für Reine und Angewandte Mathematik (in German) 55: 61–82, doi:10.1515/crll.1858.55.61, ISSN 0075-4102
Darboux, Gaston (1878), "Mémoire sur l'approximation des fonctions de très-grands nombres, et sur une classe étendue de développements en série", Journal de Mathématiques Pures et Appliquées (in French) 4: 5–56, 377–416, JFM 10.0279.01