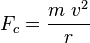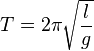Christiaan Huygens

Christiaan Huygens
Christiaan Huygens by Bernard Vaillant, Museum Hofwijck, Voorburg
Born	(1629-04-14)14 April 1629 The Hague, Dutch Republic
Died	8 July 1695(1695-07-08) (aged 66) The Hague, Dutch Republic
Residence	Netherlands, France
Nationality	Dutch
Fields	Physics Mathematics Astronomy Horology
Institutions	Royal Society of London French Academy of Sciences
Alma mater	University of Leiden University of Angers
Known for	Titan Explanation of Saturn's rings Centrifugal force Collision formulae Pendulum clock Huygens–Fresnel principle Wave theory Birefringence Evolute Huygenian eyepiece 31 equal temperament musical tuning
Influences	Galileo Galilei René Descartes Frans van Schooten
Influenced	Gottfried Wilhelm Leibniz Isaac Newton[1][2]

Christiaan Huygens, FRS (/ˈhaɪɡənz/ or /ˈhɔɪɡənz/; Dutch: [ˈɦœy̆ɣə(n)s]) (Latin: Hugenius) (14 April 1629 – 8 July 1695) was a prominent Dutch mathematician and scientist. He is known particularly as an astronomer, physicist, probabilist and horologist.

Huygens was a leading scientist of his time. His work included early telescopic studies of the rings of Saturn and the discovery of its moon Titan, the invention of the pendulum clock and other investigations in timekeeping. He published major studies of mechanics and optics, and a pioneer work on games of chance.

Early life

Christiaan Huygens was born on 14 April 1629 in The Hague, into a rich and influential Dutch family,^[3][4] the second son of Constantijn Huygens. Christiaan was named after his paternal grandfather.^[5][6] His mother was Suzanna van Baerle. She died in 1637, shortly after the birth of Huygens' sister.^[7] The couple had five children: Constantijn (1628), Christiaan (1629), Lodewijk (1631), Philips (1632) and Suzanna (1637).^[8]

Constantijn Huygens was a diplomat and advisor to the House of Orange, and also a poet and musician. His friends included Galileo Galilei, Marin Mersenne and René Descartes.^[9] Huygens was educated at home until turning sixteen years old. He liked to play with miniatures of mills and other machines. His father gave him a liberal education: he studied languages and music, history and geography, mathematics, logic and rhetoric, but also dancing, fencing and horse riding.^[5][8][10]

In 1644 Huygens had as his mathematical tutor Jan Jansz de Jonge Stampioen, who set the 15-year-old a demanding reading list on contemporary science.^[11] Descartes was impressed by his skills in geometry.^[4]

Student years

His father sent Huygens to study law and mathematics at the University of Leiden, where he studied from May 1645 to March 1647.^[5] Frans van Schooten was an academic at Leiden from 1646, and also a private tutor to Huygens and his elder brother, replacing Stampioen on the advice of Descartes.^[12][13] Van Schooten brought his mathematical education up to date, in particular introducing him to the work of Fermat on differential geometry.^[14]

After two years, from March 1647, Huygens continued his studies at the newly founded College of Orange, in Breda, where his father was a curator: the change occurred because of a duel between his brother Lodewijk and another student.^[15] Constantijn Huygens was closely involved in the new College, which lasted only to 1669; the rector was André Rivet.^[16] Christiaan Huygens lived at the home of the jurist Johann Henryk Dauber, and had mathematics classes with the English lecturer John Pell. He completed his studies in August 1649.^[5] He then had a stint as a diplomat on a mission with Henry, Duke of Nassau. It took him to Bentheim, then Flensburg. He took off for Denmark, visited Copenhagen and Helsingør, and hoped to cross the Øresund to visit Descartes in Stockholm. It was not to be.^[17]

While his father had wished Christiaan to be a diplomat, it also was not to be. In political terms, the First Stadtholderless Period that began in 1650 meant that the House of Orange was not in power, removing Constantijn Huygens's influence. Further, the father realised that his son had no interest in such a career.^[18]

Early correspondence

Huygens generally wrote in French or Latin.^[19] While still a college student at Leiden he began a correspondence with the intelligencer Mersenne, who died quite soon afterwards in 1648.^[5] Mersenne wrote to Constantijn on his son's talent for mathematics, and flatteringly compared him to Archimedes (3 January 1647). The letters show the early interests of Huygens in mathematics. In October 1646 there is the suspension bridge, and the demonstration that a catenary is not a parabola.^[20] In 1647/8 they cover the claim of Grégoire de Saint-Vincent to squaring the circle; rectification of the ellipse; projectiles, and the vibrating string.^[21] Some of Mersenne's concerns at the time, such as the cycloid (he sent Evangelista Torricelli's treatise on the curve), the centre of oscillation, and the gravitational constant, were matters Huygens only took seriously towards the end of the 1650s.^[22] Mersenne had also written on musical theory. Huygens preferred meantone temperament; he innovated in 31 equal temperament, which was not itself a new idea but known to Francisco de Salinas, using logarithms to investigate it further and show its close relation to the meantone system.^[23]

In 1654, Huygens returned to his father's house in The Hague, and was able to devote himself entirely to research.^[5] The family had another house, not far away at Hofwijck, and he spent time there during the summer. His scholarly life did not allow him to escape bouts of depression.^[24]

Subsequently Huygens developed a broad range of correspondents, though picking up the threads after 1648 was hampered by the five-year Fronde in France. Visiting Paris in 1655, Huygens called on Ismael Boulliau to introduce himself. Then Boulliau took him to see Claude Mylon.^[25] The Parisian group of savants that had gathered around Mersenne held together into the 1650s, and Mylon, who had assumed the secretarial role, took some trouble from then on to keep Huygens in touch.^[26] Through Pierre de Carcavi Huygens corresponded in 1656 with Pierre de Fermat, whom he admired greatly, though this side of idolatry. The experience was bittersweet and even puzzling, since it became clear that Fermat had dropped out of the research mainstream, and his priority claims could probably not be made good in some cases. Besides, Huygens was looking by then to apply mathematics, while Fermat's concerns ran to purer topics.^[27]

Scientific debut

Huygens was often slow to publish his results and discoveries. In the early days his mentor Frans van Schooten was cautious for the sake of his reputation.^[28]

The first work Huygens put in print was Theoremata de quadratura (1651) in the field of quadrature. It included material discussed with Mersenne some years before, such as the fallacious nature of the squaring of the circle by Grégoire de Saint-Vincent. His preferred methods were those of Archimedes and Fermat.^[14] Quadrature was a live issue in the 1650s, and through Mylon, Huygens intervened in the discussion of the mathematics of Thomas Hobbes. Persisting in trying to explain the errors Hobbes had fallen into, he made an international reputation.^[29]

Huygens studied spherical lenses from a theoretical point of view in 1652–3, obtaining results that remained unpublished until Isaac Barrow (1669). His aim was to understand telescopes.^[30] He began grinding his own lenses in 1655, collaborating with his brother Constantijn.^[31] He designed in 1662 what is now called the Huygenian eyepiece, with two lenses, as a telescope ocular.^[32][33] Lenses were also a common interest through which Huygens could meet socially in the 1660s with Baruch Spinoza, who ground them professionally. They had rather different outlooks on science, Spinoza being the more committed Cartesian, and some of their discussion survives in correspondence.^[34] He encountered the work of Antoni van Leeuwenhoek, another lens grinder, in the field of microscopy which interested his father.^[35]

Huygens wrote the first treatise on probability theory, De ratiociniis in ludo aleae ("On Reasoning in Games of Chance", 1657).^[36] He had been told of recent work in the field by Fermat, Blaise Pascal and Girard Desargues two years earlier, in Paris.^[37] Frans van Schooten translated the original Dutch manuscript "Van Rekeningh in Spelen van Geluck" into Latin and published it in his Exercitationum mathematicarum. It deals with games of chance, in particular the problem of points. Huygens took as intuitive his appeals to concepts of a "fair game" and equitable contract, and used them set up a theory of expected values.^[38] In 1662 Sir Robert Moray sent Huygens John Graunt's life table, and in time Huygens and his brother Lodewijk worked on life expectancy.^[39]

On 3 May 1661, Huygens observed the planet Mercury transit over the Sun, using the telescope of instrument maker Richard Reeve in London, together with astronomer Thomas Streete and Reeve.^[40] Streete then debated the published record of the transit of Hevelius, a controversy mediated by Henry Oldenburg.^[41] Huygens passed to Hevelius a manuscript of Jeremiah Horrocks on the transit of Venus, 1639, which thereby was printed for the first time in 1662.^[42] In that year Huygens, who played the harpsichord, took an interest in music, and Simon Stevin's theories on it; he showed very little concern to publish his theories on consonance, some of which were lost for centuries.^[43][44] The Royal Society of London elected him a Fellow in 1663.^[45]

In France

The Montmor Academy was the form the old Mersenne circle took after the mid-1650s.^[46] Huygens took part in its debates, and supported its "dissident" faction who favoured experimental demonstration to curtail fruitless discussion, and opposed amateurish attitudes.^[47] During 1663 he made what was his third visit to Paris; the Montmor Academy closed down, and Huygens took the chance to advocate a more Baconian programme in science. In 1666 he moved to Paris and a position at Louis XIV's new French Academy of Sciences.^[48]

In Paris Huygens had an important patron and correspondent in Jean-Baptiste Colbert.^[49] His relationship with the Academy was not always easy, however, and in 1670 Huygens, seriously ill, chose Francis Vernon to carry out a donation of his papers to the Royal Society in London, should he die.^[50] Then the Franco-Dutch War took place (1672−8). England's part in it (1672–4) is thought to have damaged his relationship with the Royal Society.^[51] Robert Hooke for the Royal Society lacked the urbanity to handle the situation, in 1673.^[52]

Denis Papin was assistant to Huygens from 1671.^[53] One of their projects, which did not bear fruit directly, was the gunpowder engine.^[54] Papin moved to England in 1678, and continued to work in this area.^[55] Using the Paris Observatory (completed in 1672), Huygens made further astronomical observations. In 1678 he introduced Nicolaas Hartsoeker to French scientists such as Nicolas Malebranche and Giovanni Cassini.

It was in Paris, also, that Huygens met the young diplomat Gottfried Leibniz, there in 1672 on a vain mission to meet Arnauld de Pomponne, the French Foreign Minister. At this time Leibniz was working on a calculating machine, and he moved on to London in early 1673 with diplomats from Mainz; but from March 1673 Leibniz was tutored in mathematics by Huygens.^[56] Huygens taught him analytical geometry; an extensive correspondence ensued, in which Huygens showed reluctance to accept the advantages of infinitesimal calculus.^[57]

Later life

Huygens moved back to The Hague in 1681 after suffering serious depressive illness. In 1684, he published Astroscopia Compendiaria on his new tubeless aerial telescope. He attempted to return to France in 1685 but the revocation of the Edict of Nantes precluded this move. His father died in 1687, and he inherited Hofwijck, which he made his home the following year.^[18]

On his third visit to England, in 1689, Huygens met Isaac Newton on 12 June. They spoke about Iceland spar, and subsequently corresponded about resisted motion.^[58]

Huygens observed the acoustical phenomenon now known as flanging in 1693.^[59] He died in The Hague on 8 July 1695, and was buried in the Grote Kerk.^[60]

Work in natural philosophy

Huygens has been called the leading European natural philosopher between Descartes and Newton.^[61] He adhered to the tenets of the mechanical philosophy of his time. In particular he sought explanations of the force of gravity that avoided action at a distance.^[62]

In common with Robert Boyle and Jacques Rohault, Huygens adhered to what has been called, more explicitly, "experimentally oriented corpuscular-mechanical" natural philosophy. In the analysis of the Scientific Revolution this appears as a mainstream position, at least from the founding of the Royal Society to the emergence of Newton, and was sometimes labelled "Baconian", while not being inductivist or identifying with the views of Francis Bacon in a simple-minded way.^[63] After his first visit to England in 1661, when he attended a meeting of the Gresham College group in April and learned directly about Boyle's air pump experiments, Huygens spent time in late 1661 and early 1662 replicating the work. It proved a long process, brought to the surface an experimental issue ("anomalous suspension") and the theoretical issue of horror vacui, and ended in July 1663 as Huygens became a Fellow of the Royal Society. It has been said that Huygens finally accepted Boyle's view of the void, as against the Cartesian denial of it;^[64] and also (in Leviathan and the Air Pump) that the replication of results trailed off messily.^[65]

Newton's influence on John Locke was mediated by Huygens, who assured Locke that Newton's mathematics was sound, leading to Locke's acceptance of a "corpuscular-mechanical" physics.^[66]

Laws of motion, impact and gravitation

The general approach of the mechanical philosophers was to postulate theories of the kind now called "contact action". Huygens adopted this method, but not without seeing its difficulties and failures.^[67] Leibniz, his student in Paris, abandoned the theory.^[68] Seeing the universe this way made the theory of collisions central to physics. The requirements of the mechanical philosophy, in the view of Huygens, were stringent. Matter in motion made up the universe, and only explanations in those terms could be truly intelligible. While he was influenced by the Cartesian approach, he was less doctrinaire.^[69] He studied elastic collisions in the 1650s but delayed publication for over a decade.^[14]

Huygens concluded quite early that Descartes's laws for the elastic collision of two bodies must be wrong, and he formulated the correct laws.^[70] An important step was his recognition of the Galilean invariance of the problems.^[71] His views then took many years to be circulated. He passed them on in person to William Brouncker and Christopher Wren in London, in 1661.^[72] What Spinoza wrote to Henry Oldenburg about them, in 1666 which was during the Second Anglo-Dutch War, was guarded.^[73] Huygens had actually worked them out in a manuscript De motu corporum ex percussione in the period 1652–6. The war ended in 1667, and Huygens announced his results to the Royal Society in 1668. He published them in the Journal des sçavans in 1669.^[14]

Huygens stated what is now known as the second of Newton's laws of motion in a quadratic form.^[74] In 1659 he derived the now standard formula for the centripetal force, exerted by an object describing a circular motion, for instance on the string to which it is attached. In modern notation:

with m the mass of the object, v the velocity and r the radius. The publication of the general formula for this force in 1673 was a significant step in studying orbits in astronomy. It enabled the transition from Kepler's third law of planetary motion, to the inverse square law of gravitation.^[75] The interpretation of Newton's work on gravitation by Huygens differed, however, from that of Newtonians such as Roger Cotes; he did not insist on the a priori attitude of Descartes, but neither would he accept aspects of gravitational attractions that were not attributable in principle to contact of particles.^[76]

The approach used by Huygens also missed some central notions of mathematical physics, which were not lost on others. His work on pendulums came very close to the theory of simple harmonic motion; but the topic was covered fully for the first time by Newton, in Book II of his Principia Mathematica (1687).^[77] In 1678 Leibniz picked out of Huygens's work on collisions the idea of conservation law that Huygens had left implicit.^[78]

Optics

Huygens is remembered especially for his wave theory of light, which he first communicated in 1678 to the Paris Académie des sciences. It was published in 1690 in his Traité de la lumière (Treatise on light).^[79] He refers to Ignace-Gaston Pardies, whose manuscript on optics helped him on his wave theory.^[80]

A basic principle of Huygens is that the speed of light is finite, a point which had been the subject of an experimental demonstration by Olaus Roemer (1679 at the Paris Observatory), but which Huygens is presumed to have believed already.^[81] The theory is kinematic and its scope largely restricted to geometric optics. It covers little of what would now be termed physical optics. It deals with wave fronts and their normal rays, with propagation conceived by means of spherical waves emitted along the wave front (see also Huygens–Fresnel principle).^[82] It was justified as an ether theory, involving transmission via perfectly elastic particles, a revision of the view of Descartes. The nature of light was therefore a longitudinal wave.^[81]

Huygens had experimented in 1672 with double refraction (birefringence) in Icelandic spar (calcite), a phenomenon discovered in 1669 by Rasmus Bartholin. At first he could not elucidate what he found.^[33] He later explained it with his wave front theory and concept of evolutes. He also developed ideas on caustics.^[83] Newton in his Opticks of 1704 proposed instead a corpuscular theory of light. The theory of Huygens was not accepted, by some, because longitudinal waves cannot show birefringence. The interference experiments of Thomas Young vindicated a wave theory in 1801: the results could not be explained with light particles. The solution to the problem Huygens had faced was then resolved by a transverse wave theory.^[84] For a view from modern physics see wave–particle duality.

Huygens investigated the use of lenses in projectors. He is credited as the inventor of the magic lantern, described in correspondence of 1659.^[85] There are others to whom such a lantern device has been attributed, such as Giambattista della Porta, and Cornelis Drebbel: the point at issue is the use of a lens for better projection. Athanasius Kircher has also been credited for that.^[86]

Horology

Huygens designed more accurate clocks than were available at the time. His invention of the pendulum clock was a breakthrough in timekeeping, and he made a prototype by the end of 1656. In 1657 he contracted the construction of his designs to Salomon Coster in The Hague, with a local patent (octroy). He was less successful elsewhere: Pierre Séguier refused him any French rights, Simon Douw of Rotterdam copied the design in 1658, and Ahasuerus Fromanteel also, in London.^[87] The oldest known Huygens-style pendulum clock is dated 1657 and can be seen at the Museum Boerhaave in Leiden.^{[88][89][90][91]}

The new clock was potentially suitable for navigational uses (longitude by chronometer). Exploiting the invention at sea proved troublesome, however. In 1660 Lodewijk Huygens made a trial on a voyage to Spain, and reported that heavy weather made the clock useless. Alexander Bruce elbowed into the field in 1662, and Huygens called in Sir Robert Moray and the Royal Society to mediate and preserve some of his rights.^[92] Trials continued into the 1660s, the best news coming from a Royal Navy captain Robert Holmes operating against the Dutch possessions in 1664.^[93] Lisa Jardine ^[94] doubts that Holmes reported the results of the trial accurately, and Samuel Pepys expressed his doubts at the time: The said master [i.e. the captain of Holmes' ship] affirmed, that the vulgar reckoning proved as near as that of the watches, which [the clocks], added he, had varied from one another unequally, sometimes backward, sometimes forward, to 4, 6, 7, 3, 5 minutes; as also that they had been corrected by the usual account. One for the French Academy on an expedition to Cayenne ended badly. Jean Richer suggested correction for the figure of the Earth. By the time of the Dutch East India Company expedition of 1686 to the Cape of Good Hope, Huygens was able to supply the correction retrospectively.^[95]

Pendulums

In 1673 Huygens published Horologium Oscillatorium sive de motu pendulorum, his major work on pendulums and horology. It had been observed by Mersenne and others that pendulums are not quite isochronous: their period depends on their width of swing, with wide swings taking slightly longer than narrow swings.^[98][99]

Huygens analyzed this problem by finding the curve down which a mass will slide under the influence of gravity in the same amount of time, regardless of its starting point; the so-called tautochrone problem. By geometrical methods which were an early use of calculus, he showed it to be a cycloid, rather than the circular arc of a pendulum's bob, and therefore that pendulums are not isochronous. He also solved a problem posed by Mersenne: how to calculate the period of a pendulum made of an arbitrarily shaped swinging rigid body. This involved discovering the center of oscillation and its reciprocal relationship with the pivot point. In the same work, he analysed the conical pendulum, consisting of a weight on a cord moving in a circle, using the concept of centrifugal force.

Huygens was the first to derive the formula for the period of an ideal mathematical pendulum (with massless rod or cord and length much longer than its swing), in modern notation:

with T the period, l the length of the pendulum and g the gravitational acceleration. By his study of the oscillation period of compound pendulums Huygens made pivotal contributions to the development of the concept of moment of inertia.^[74]

Huygens also observed coupled oscillations: two of his pendulum clocks mounted next to each other on the same support often became synchronized, swinging in opposite directions. He reported the results by letter to the Royal Society, and it is referred to as "an odd kind of sympathy" in the Society's minutes.^[100][101] This concept is now known as entrainment.

Balance spring watch

Huygens developed a balance spring watch in the same period as, though independently of, Robert Hooke. Controversy over the priority persisted for centuries. A Huygens watch employed a spiral balance spring; but he used this form of spring initially only because the balance in his first watch rotated more than one and a half turns. He later used spiral springs in more conventional watches, made for him by Thuret in Paris from around 1675.

Such springs were essential in modern watches with a detached lever escapement because they can be adjusted for isochronism. Watches in the time of Huygens and Hooke, however, employed the very undetached verge escapement. It interfered with the isochronal properties of any form of balance spring, spiral or otherwise.

In February 2006, a long-lost copy of Hooke's handwritten notes from several decades of Royal Society meetings was discovered in a cupboard in Hampshire, England. The balance-spring priority controversy appears, by the evidence contained in those notes, to be settled in favour of Hooke's claim.^[102][103]

In 1675, Huygens patented a pocket watch. The watches which were made in Paris from c. 1675 and following the Huygens plan are notable for lacking a fusee for equalizing the mainspring torque. The implication is that Huygens thought that his spiral spring would isochronise the balance, in the same way that he thought that the cycloidally shaped suspension curbs on his clocks would isochronise the pendulum.

Astronomy

Saturn's rings and Titan

In 1655, Huygens proposed that Saturn was surrounded by a solid ring, "a thin, flat ring, nowhere touching, and inclined to the ecliptic." Using a 50 power refracting telescope that he designed himself, Huygens also discovered the first of Saturn's moons, Titan.^[104] In the same year he observed and sketched the Orion Nebula. His drawing, the first such known of the Orion nebula, was published in Systema Saturnium in 1659. Using his modern telescope he succeeded in subdividing the nebula into different stars. The brighter interior now bears the name of the Huygenian region in his honour.^[105] He also discovered several interstellar nebulae and some double stars.

Cosmotheoros

Shortly before his death in 1695, Huygens completed Cosmotheoros, published posthumously in 1698. In it he speculated on the existence of extraterrestrial life, on other planets, which he imagined was similar to that on Earth.

Such speculations were not uncommon at the time, justified by Copernicanism or the plenitude principle. But Huygens went into greater detail.^[106] The work, translated into English in its year of publication, has been seen as in the fanciful tradition of Francis Godwin, John Wilkins and Cyrano de Bergerac, and fundamentally Utopian; and also to owe in its concept of planet to cosmography in the sense of Peter Heylin.^[107][108]

Huygens wrote that availability of water in liquid form was essential for life and that the properties of water must vary from planet to planet to suit the temperature range. He took his observations of dark and bright spots on the surfaces of Mars and Jupiter to be evidence of water and ice on those planets.^[109] He argued that extraterrestrial life is neither confirmed nor denied by the Bible, and questioned why God would create the other planets if they were not to serve a greater purpose than that of being admired from Earth. Huygens postulated that the great distance between the planets signified that God had not intended for beings on one to know about the beings on the others, and had not foreseen how much humans would advance in scientific knowledge.^[110]

It was also in this book that Huygens published his method for estimating stellar distances. He made a series of smaller holes in a screen facing the sun, until he estimated the light was of the same intensity as that of the star Sirius. He then calculated that the angle of this hole was 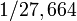th the diameter of the Sun, and thus it was about 30,000 times as far away, on the (incorrect) assumption that Sirius is as bright as our sun. The subject of photometry remained in its infancy until Pierre Bouguer and Johann Heinrich Lambert.^[111]

Works

• 1649 – De iis quae liquido supernatant (About the parts above the water, unpublished)
• 1651 – Cyclometriae
• 1651 – Theoremata de quadratura hyperboles, ellipsis et circuli, in Oeuvres Complètes, Tome XI, link from Internet Archive.
• 1654 – De circuli magnitudine inventa
• 1656 – De Saturni Luna observatio nova (About the new observation of the moon of Saturn – discovery of Titan)
• 1656 – De motu corporum ex percussione, published only in 1703
• 1657 – De ratiociniis in ludo aleae = Van reeckening in spelen van geluck (translated by Frans van Schooten)
• 1659 – Systema saturnium (on the planet Saturn)
• 1659 – De vi centrifuga (Concerning the centrifugal force), published in 1703
• 1673 – Horologium oscillatorium sive de motu pendularium (theory and design of the pendulum clock, dedicated to Louis XIV of France)
• 1684 – Astroscopia Compendiaria tubi optici molimine liberata (compound telescopes without a tube)
• 1685 – Memoriën aengaende het slijpen van glasen tot verrekijckers (How to grind telescope lenses)
• 1686 – Old Dutch: Kort onderwijs aengaende het gebruijck der horologiën tot het vinden der lenghten van Oost en West (How to use clocks to establish the longitude)
• 1690 – Traité de la lumière
• 1690 – Discours de la cause de la pesanteur (Discourse about gravity, from 1669?)
• 1691 – Lettre touchant le cycle harmonique (Rotterdam, concerning the 31-tone system)
• 1698 – Cosmotheoros (solar system, cosmology, life in the universe)
• 1703 – Opuscula posthuma including
  • De motu corporum ex percussione (Concerning the motions of colliding bodies – contains the first correct laws for collision, dating from 1656).
  • Descriptio automati planetarii (description and design of a planetarium)
• 1724 – Novus cyclus harmonicus (Leiden, after Huygens' death)
• 1728 – Christiani Hugenii Zuilichemii, dum viveret Zelhemii toparchae, opuscula posthuma ... (pub. 1728) Alternate title: Opera reliqua, concerning optics and physics

• 1888–1950 – Huygens, Christiaan. Oeuvres complètes. The Hague Complete work, editors D. Bierens de Haan (tome=deel 1-5), J. Bosscha (6-10), D.J. Korteweg (11-15), A.A. Nijland (15), J.A. Vollgraf (16-22).

Tome I: Correspondance 1638–1656 (1888). Tome II: Correspondance 1657–1659 (1889). Tome III: Correspondance 1660–1661 (1890). Tome IV: Correspondance 1662–1663 (1891). Tome V: Correspondance 1664–1665 (1893). Tome VI: Correspondance 1666–1669 (1895). Tome VII: Correspondance 1670–1675 (1897). Tome VIII: Correspondance 1676–1684 (1899). Tome IX: Correspondance 1685–1690 (1901). Tome X: Correspondance 1691–1695 (1905).

Tome XI: Travaux mathématiques 1645–1651 (1908). Tome XII: Travaux mathématiques pures 1652–1656 (1910).

Tome XIII, Fasc. I: Dioptrique 1653, 1666 (1916). Tome XIII, Fasc. II: Dioptrique 1685–1692 (1916).

Tome XIV: Calcul des probabilités. Travaux de mathématiques pures 1655–1666 (1920).

Tome XV: Observations astronomiques. Système de Saturne. Travaux astronomiques 1658–1666 (1925).

Tome XVI: Mécanique jusqu’à 1666. Percussion. Question de l'existence et de la perceptibilité du mouvement absolu. Force centrifuge (1929). Tome XVII: L’horloge à pendule de 1651 à 1666. Travaux divers de physique, de mécanique et de technique de 1650 à 1666. Traité des couronnes et des parhélies (1662 ou 1663) (1932). Tome XVIII: L'horloge à pendule ou à balancier de 1666 à 1695. Anecdota (1934). Tome XIX: Mécanique théorique et physique de 1666 à 1695. Huygens à l'Académie royale des sciences (1937).

Tome XX: Musique et mathématique. Musique. Mathématiques de 1666 à 1695 (1940).

Tome XXI: Cosmologie (1944).

Tome XXII: Supplément à la correspondance. Varia. Biographie de Chr. Huygens. Catalogue de la vente des livres de Chr. Huygens (1950).

Portraits

During his lifetime

• 1639 – His father Constantijn Huygens in the midst of his five children by Adriaen Hanneman, painting with medaillons, Mauritshuis, The Hague
• 1671 – Portrait by Caspar Netscher, Museum Boerhaave, Leiden, loan from Haags Historisch Museum
• ~1675 – Possible depiction of Huygens on l'French: Établissement de l'Académie des Sciences et fondation de l'observatoire, 1666 by Henri Testelin. Colbert presents the members of the newly founded Académie des Sciences to king Louis XIV of France. Musée National du Château et des Trianons de Versailles, Versailles
• 1679 – Medaillon portrait in relief by the French sculptor Jean-Jacques Clérion
• 1686 – Portrait in pastel by Bernard Vaillant, Museum Hofwijck, Voorburg
• between 1684 and 1687 – Engraving by G. Edelinck after the painting by Caspar Netscher
• 1688 – Portrait by Pierre Bourguignon (painter), Koninklijke Nederlandse Akademie van Wetenschappen, Amsterdam

Named after Huygens

Science

• The Huygens probe: The lander for the Saturnian moon Titan, part of the Cassini–Huygens mission to Saturn
• Asteroid 2801 Huygens
• A crater on Mars
• Mons Huygens, a mountain on the Moon
• Huygens Software, a microscope image processing package.
• A two element eyepiece designed by him. An early step in the development of the achromatic lens, since it corrects some chromatic aberration.
• The Huygens–Fresnel principle, a simple model to understand disturbances in wave propagation.
• Huygens wavelets, the fundamental mathematical basis for scalar diffraction theory
• W.I.S.V. Christiaan Huygens: Dutch study guild for the studies Mathematics and Computer Science at the Delft University of Technology
• Huygens Laboratory: Home of the Physics department at Leiden University, Netherlands
• Huygens Supercomputer: National Supercomputer facility of the Netherlands, located at SARA in Amsterdam
• The Huygens-building in Noordwijk, Netherlands, first building on the Space Business park opposite Estec (ESA)
• The Huygens-building at the Radboud University, Nijmegen, The Netherlands. One of the major buildings of the science department at the university of Nijmegen.

Other

• Christiaan Huygens College, High School located in Eindhoven, Netherlands.
• The Christiaan Huygens, a ship of the Nederland Line.
• Huygens Scholarship Programme for international students and Dutch students

See also

• History of the internal combustion engine
• List of largest optical telescopes historically

References

• Bell, A. E. (1947). Christian Huygens and the Development of Science in the Seventeenth Century. Edward Arnold & Co, London. 
• Daniel Garber (2003). The Cambridge History of Seventeenth-century Philosophy (2 vols.). Cambridge University Press. ISBN 978-0-521-53720-9. Retrieved 11 May 2013. 
• Alan E. Shapiro, Kinematic Optics: A Study of the Wave Theory of Light in the Seventeenth Century, Archive for History of Exact Sciences Vol. 11, No. 2/3 (31.XII.1973), pp. 134-266. Published by: Springer. Stable URL: http://www.jstor.org/stable/41133375
• Wiep van Bunge et al. (editors), The Dictionary of Seventeenth and Eighteenth-Century Dutch Philosophers (2003), Thoemmes Press (two volumes), article Huygens, Christiaan, p. 468–77.

Notes

Further reading

• Andriesse, C.D., 2005, Huygens: The Man Behind the Principle. Foreword by Sally Miedema. Cambridge University Press.
• Boyer, C.B.: A history of mathematics, New York, 1968
• Dijksterhuis, E. J.: The Mechanization of the World Picture: Pythagoras to Newton
• Hooijmaijers, H.: Telling time – Devices for time measurement in Museum Boerhaave – A Descriptive Catalogue, Leiden, Museum Boerhaave, 2005
• Struik, D.J.: A history of mathematics
• Van den Ende, H. et al.: Huygens's Legacy, The golden age of the pendulum clock, Fromanteel Ltd, Castle Town, Isle of Man, 2004
• Yoder, J G., 2005, "Book on the pendulum clock" in Ivor Grattan-Guinness, ed., Landmark Writings in Western Mathematics. Elsevier: 33-45.
• Christiaan Huygens (1629–1695) : Library of Congress Citations. Retrieved 2005-03-30.

External links

Wikimedia Commons has media related to Christiaan Huygens.

Wikiquote has quotations related to: Christiaan Huygens

Primary sources, translations

• Works by Christiaan Huygens at Project Gutenberg
  • Treatise on Light translated into English by Silvanus P. Thompson, Project Gutenberg etext.
• Works by or about Christiaan Huygens at Internet Archive
• Works by Christiaan Huygens at LibriVox (public domain audiobooks)
• De Ratiociniis in Ludo Aleae or The Value of all Chances in Games of Fortune, 1657 Christiaan Huygens' book on probability theory. An English translation published in 1714. Text pdf file.
• Horologium oscillatorium (German translation, pub. 1913) or Horologium oscillatorium (English translation by Ian Bruce) on the pendulum clock
• ΚΟΣΜΟΘΕΩΡΟΣ (Cosmotheoros). (English translation of Latin, pub. 1698; subtitled The celestial worlds discover'd: or, Conjectures concerning the inhabitants, plants and productions of the worlds in the planets.)
• Traité de la lumière or Treatise on light (English translation, pub. 1912 and again in 1962)
• Systema Saturnium 1659 text a digital edition of Smithsonian Libraries
• On Centrifugal Force (1703)
• Huygens' work at WorldCat
• Christiaan Huygens biography and achievements
• Portraits of Christiaan Huygens

Museums

• Huygensmuseum Hofwijck in Voorburg, Netherlands, where Huygens lived and worked.
• Huygens Clocks exhibition from the Science Museum, London
• LeidenUniv.nl, Exhibition on Huygens in University Library Leiden (Dutch)

Other

• O'Connor, John J.; Robertson, Edmund F., "Christiaan Huygens", MacTutor History of Mathematics archive, University of St Andrews .
• Huygens and music theory Huygens–Fokker Foundation —on Huygens' 31 equal temperament and how it has been used
• Christiaan Huygens on the 25 Dutch Guilder banknote of the 1950s.
• Christiaan Huygens at the Mathematics Genealogy Project
• How to pronounce "Huygens"

Authority control WorldCat VIAF: 9894043 LCCN: n79134100 ISNI: 0000 0001 0868 7618 GND: 118639749 SUDOC: 030533023 BNF: cb12192922r (data) BPN: 19453564 ULAN: 500026922 MGP: 125561 RKD: 40795

Microtonal music People Easley Blackwood, Jr. Heinz Bohlen Wendy Carlos Julián Carrillo Mildred Couper Ivor Darreg John Eaton Adriaan Fokker Alois Hába Lou Harrison Christiaan Huygens Ben Johnston Joel Mandelbaum Joe Maneri Harry Partch Ezra Sims Nicola Vicentino Elaine Walker Ivan Wyschnegradsky Tunings & scales Non-octave- repeating scales Alpha scale Beta scale Gamma scale Delta scale Lambda scale (Bohlen–Pierce scale) Equal temperament 15 17 19 22 24 31 34 41 53 72 Just intonation Harry Partch's 43-tone scale Concepts & techniques Limit Otonality and Utonality Semitone Sonido 13 Xenharmonic music Groups & publications Boston Microtonal Society Genesis of a Music Huygens-Fokker Foundation Tonalsoft Xenharmonic Bulletin Compositions Beauty in the Beast quarter tone pieces just pieces Mother Sonata for Microtonal Piano Suite for Microtonal Piano Twelve Microtonal Etudes for Electronic Music Media Other Enharmonic keyboard Generalized keyboard Modernism (music)