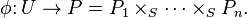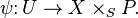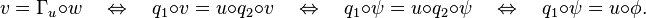Chow's lemma
Chow's lemma, named after Wei-Liang Chow, is one of the foundational results in algebraic geometry. It roughly says that a proper morphism is fairly close to being a projective morphism. More precisely, a version of it states the following:[1]
- If
 is a scheme that is proper over a noetherian base
is a scheme that is proper over a noetherian base  , then there exists a projective
, then there exists a projective  -scheme
-scheme 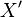 and a surjective
and a surjective  -morphism
-morphism 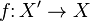 that induces an isomorphism
that induces an isomorphism 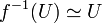 for some dense open
for some dense open 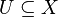 .
.
Proof
The proof here is a standard one (cf. EGA II, 5.6.1).
It is easy to reduce to the case when  is irreducible, as follows.
is irreducible, as follows.  is noetherian since it is of finite type over a noetherian base. Then it's also topologically noetherian, and consists of a finite number of irreducible components
is noetherian since it is of finite type over a noetherian base. Then it's also topologically noetherian, and consists of a finite number of irreducible components  , which are each proper over
, which are each proper over  (because they're closed immersions in the scheme
(because they're closed immersions in the scheme  which is proper over
which is proper over  ). If, within each of these irreducible components, there exists a dense open
). If, within each of these irreducible components, there exists a dense open 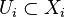 , then we can take
, then we can take 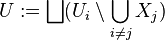 . It is not hard to see that each of the disjoint pieces are dense in their respective
. It is not hard to see that each of the disjoint pieces are dense in their respective  , so the full set
, so the full set  is dense in
is dense in  . In addition, it's clear that we can similarly find a morphism
. In addition, it's clear that we can similarly find a morphism  which satisfies the density condition.
which satisfies the density condition.
Having reduced the problem, we now assume  is irreducible. We recall that it must also be noetherian. Thus, we can find a finite open affine cover
is irreducible. We recall that it must also be noetherian. Thus, we can find a finite open affine cover 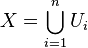 .
. 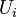 are quasi-projective over
are quasi-projective over  ; there are open immersions over
; there are open immersions over  ,
, 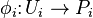 into some projective
into some projective  -schemes
-schemes 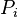 . Put
. Put 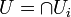 .
.  is nonempty since
is nonempty since  is irreducible. Let
is irreducible. Let
be given by 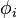 's restricted to
's restricted to  over
over  .
Let
.
Let
be given by 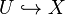 and
and  over
over  .
. 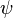 is then an immersion; thus, it factors as an open immersion followed by a closed immersion
is then an immersion; thus, it factors as an open immersion followed by a closed immersion 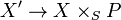 . Let
. Let 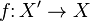 be the immersion followed by the projection. We claim
be the immersion followed by the projection. We claim  induces
induces 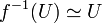 ; for that, it is enough to show
; for that, it is enough to show 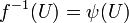 . But this means that
. But this means that 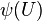 is closed in
is closed in 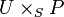 .
. 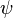 factorizes as
factorizes as 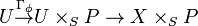 .
.  is separated over
is separated over  and so the graph morphism
and so the graph morphism 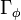 is a closed immersion. This proves our contention.
is a closed immersion. This proves our contention.
It remains to show 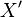 is projective over
is projective over  . Let
. Let 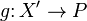 be the closed immersion followed by the projection. Showing that
be the closed immersion followed by the projection. Showing that  is a closed immersion shows
is a closed immersion shows 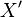 is projective over
is projective over  . This can be checked locally. Identifying
. This can be checked locally. Identifying 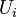 with its image in
with its image in 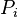 we suppress
we suppress 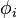 from our notation.
from our notation.
Let 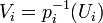 where
where 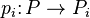 . We claim
. We claim 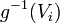 are an open cover of
are an open cover of 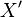 . This would follow from
. This would follow from 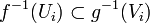 as sets. This in turn follows from
as sets. This in turn follows from 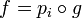 on
on 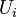 as functions on the underlying topological space. Since
as functions on the underlying topological space. Since  is separated over
is separated over  and
and 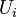 is dense, this is clear from looking at the relevant commutative diagram. Now,
is dense, this is clear from looking at the relevant commutative diagram. Now, 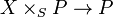 is closed since it is a base extension of the proper morphism
is closed since it is a base extension of the proper morphism 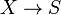 . Thus,
. Thus, 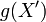 is a closed subscheme covered by
is a closed subscheme covered by 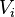 , and so it is enough to show that for each
, and so it is enough to show that for each  the map
the map 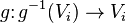 , denoted by
, denoted by 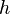 , is a closed immersion.
, is a closed immersion.
Fix  . Let
. Let  be the graph of
be the graph of 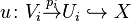 . It is a closed subscheme of
. It is a closed subscheme of 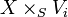 since
since  is separated over
is separated over  . Let
. Let 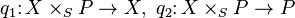 be the projections. We claim that
be the projections. We claim that 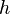 factors through
factors through  , which would imply
, which would imply 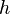 is a closed immersion. But for
is a closed immersion. But for 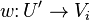 we have:
we have:
The last equality holds and thus there is 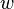 that satisfies the first equality. This proves our claim.
that satisfies the first equality. This proves our claim. 
Additional statements
In the statement of Chow's lemma, if  is reduced, irreducible, or integral, we can assume that the same holds for
is reduced, irreducible, or integral, we can assume that the same holds for 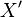 . If both
. If both  and
and 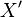 are irreducible, then
are irreducible, then 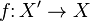 is a birational morphism. (cf. EGA II, 5.6).
is a birational morphism. (cf. EGA II, 5.6).
References
- ↑ Hartshorne, Ch II. Exercise 4.10
- Grothendieck, Alexandre; Dieudonné, Jean (1961). "Éléments de géométrie algébrique: II. Étude globale élémentaire de quelques classes de morphismes". Publications Mathématiques de l'IHÉS 8. doi:10.1007/bf02699291. MR 0217084.
- Hartshorne, Robin (1977), Algebraic Geometry, Graduate Texts in Mathematics 52, New York: Springer-Verlag, ISBN 978-0-387-90244-9, MR 0463157