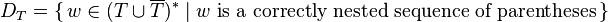Chomsky–Schützenberger representation theorem

In formal language theory, the Chomsky–Schützenberger representation theorem is a theorem derived by Noam Chomsky and Marcel-Paul Schützenberger about representing a given context-free language in terms of two simpler languages. These two simpler languages, namely a regular language and a Dyck language, are combined by means of an intersection and a homomorphism.

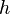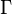A few notions from formal language theory are in order. A context-free language is regular, if can be described by a regular expression, or, equivalently, if it is accepted by a finite automaton. 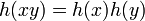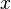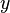A homomorphism is based on a function h which maps symbols from an alphabet \Gamma to words over another alphabet \Sigma; If the domain of this function is extended to words over \Gamma in the natural way, by letting h(xy)=h(x)h(y) for all words x and y, this yields a homomorphism 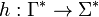h:\Gamma^*\to \Sigma^*. A matched alphabet 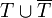T \cup \overline T is an alphabet with two equal-sized sets; it is convenient to think of it as a set of parentheses types, where 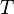T contains the opening parenthesis symbols, whereas the symbols in 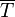\overline T contains the closing parenthesis symbols. For a matched alphabet 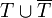T \cup \overline T, the Dyck language 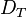D_T is given by

D_T = \{\,w \in (T \cup \overline T)^* \mid w \text{ is a correctly nested sequence of parentheses} \,\}

words that are well-nested parentheses over 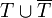T \cup \overline T.

Chomsky–Schützenberger theorem. A language L over the alphabet 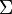\Sigma is context-free if and only if there exists
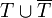
  • a matched alphabet T \cup \overline T
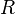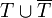  • a regular language R over T \cup \overline T,
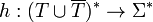
  • and a homomorphism h : (T \cup \overline T)^* \to \Sigma^*
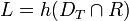such that L = h(D_T \cap R).

Proofs of this theorem are found in several textbooks, e.g. Autebert, Berstel & Boasson (1997) or Davis, Sigal & Weyuker (1994).

References