Chiral homology
In mathematics, chiral homology, introduced by Beilinson−Drinfeld, is, in their words, "a “quantum” version of (the algebra of functions on) the space of global horizontal sections of an affine 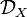 -scheme (i.e., the space of global solutions of a system of non-linear differential equations)."
-scheme (i.e., the space of global solutions of a system of non-linear differential equations)."
Lurie's topological chiral homology gives a generalization.[1]